The Lord created certain types of fundamental particles and also determined the rules these particles obey. These are what allow for the rich diversity of substances in the universe today. We here consider baryons – the substance of the cosmos. We will find that baryons confirm biblical creation and challenge secular explanations.
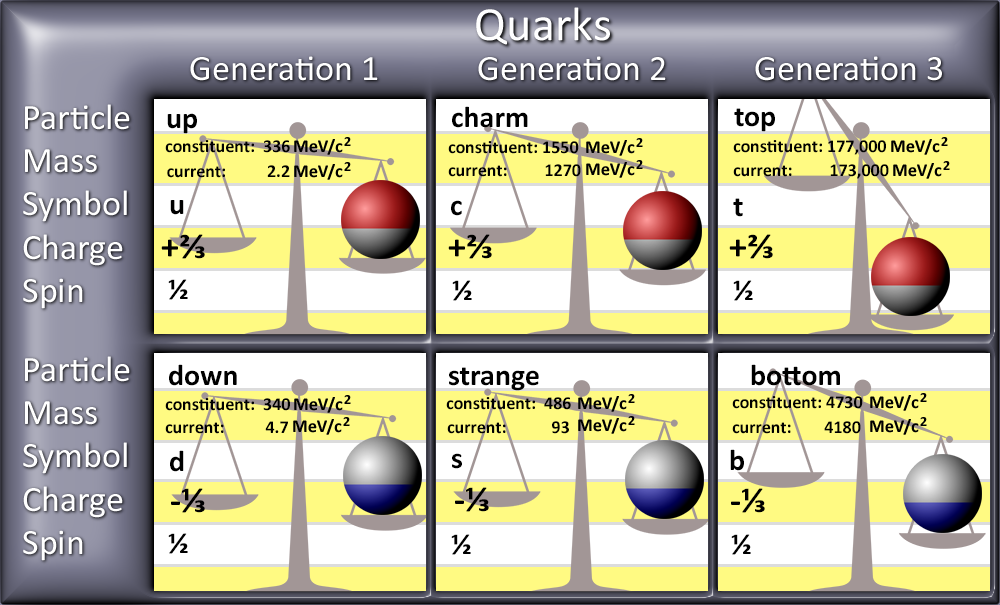
In the previous article we examined elementary particles called quarks. Quarks are spin-½ fermions that come in six flavors and have fractional electric charge. Recall, the up quark has an electric charge of +2/3, whereas the down quark has a charge of -1/3. Quarks and antiquarks are the only known particles with fractional charge. We also saw that quarks respond to the strong force – a force somewhat like the electric force, except much stronger and with extremely limited range. The strong force has six types of “color charge” which we label as red, green, blue, anti-red, anti-green, and anti-blue. These have nothing to do with visual colors, but they “add” the same way colors do. Quarks always come with one of the three positive-type color charges (red, green, or blue), and any one of these will attract the other two. For this reason, quarks tend to come in groups of three (one red, one green, and one blue) to form a color-neutral particle.
A baryon is any particle made of exactly three bound quarks.[1] Each quark comes in one of two possible spin states, +½ (spin up), or -½ (spin down). And since there are three quarks, the total spin state of a baryon will be the sum of the spin states of its quarks: -3/2, -½, +½, or +3/2. Thus, the magnitude of the spin of a baryon is either ½, or 3/2.[2] Since they have non-integer spin, all baryons are fermions and obey the Pauli exclusion principle – they cannot be in the same quantum state at the same time. All baryons are color neutral because they have one red quark, one green quark, and one blue quark. Yet, they can bind to other baryons by the residual strong force due to their constituent quarks.
Mass Defect
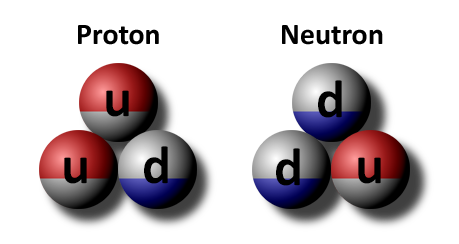
The two baryons we are most familiar with are the proton and neutron with composition uud (up, up, and down quarks) and udd (up, down, and down quarks) respectively. So, for the proton, if we add the (constituent) masses of the two up quarks with the one down quark we get 1012 MeV/c2. Yet, many experiments have revealed the mass of the proton to be 938 MeV/c2. The whole is less than the sum of its parts! Where did the other 74 MeV/c2 go? In the previous article, we found that the electron has some mass due to its self-repelling charge. That is, it would take energy to force a cloud of negative charge into such a small volume because it is mutually repulsive. That energy has mass and therefore makes the electron heavier than the electron neutrino. In the case of the three quarks in a proton, they are attracted to each other due to the strong force. It is the opposite situation because it would take energy to pull them away. Thus, they have less energy in the bound state than they would have if we could somehow separate them. That binding energy is negative; therefore, it reduces the mass of the system. This is called mass defect.
Any system in which the particles are bound by an attractive force will have less mass than if the same particles could be separated.[3] The strong force is so powerful, the energy associated with it is often comparable to the mass of the particles involved. Therefore, we cannot assume that the mass of a composite particle will be merely the sum of the masses of its components. We must include negative contributions from binding energy, as well as positive energy contributions of motion, aligned spin states, and so on.
Consider a helium nucleus. It contains two protons and two neutrons. If we add the mass of two protons and two neutrons, we get 3755.7 MeV/c2. Yet, the mass of the helium nucleus is 3726.7 MeV/c2. So, the mass defect is 29 MeV/c2. That means it would take 29 MeV of energy to separate the four particles in a helium nucleus. This also means that if we could bring together two protons and two neutrons into a helium nucleus, this process would release 29 MeV of energy per helium atom. This is how nuclear fusion works. In the core of the sun, hydrogen is constantly being fused into helium, releasing an enormous amount of energy.
Likewise, the mass of baryons is determined primarily by the constituent mass of their quarks, but is also affected by the internal energy of the system. Consider the neutral delta baryon. It is made of one up quark and two down quarks. That is exactly the same quark composition as a neutron. Yet, the neutral delta has a mass of 1232 MeV/c2, whereas the neutron has a mass of only 940 MeV/c2. The neutral delta has greater internal energy because all three of its quarks have the same (aligned) spin state, whereas the neutron has one quark anti-aligned with the other two. The spin of the baryon is the sum of the spin states of its constituent particles.[4] So, the neutron has a spin of ½, but the delta has a spin of 3/2. The delta is a fundamentally different particle with different properties from the neutron even though they have identical quark compositions!
Families of Baryons
Baryons fall into six natural families based on both their quark composition and the spin states of their quarks. These spin states affect the total mass and the total spin of the resulting baryon. Protons and neutrons are the only two members of the nucleon family.[5] Nucleons are baryons consisting only of up and down quarks, where the spin of one quark is anti-aligned with the other two. Nucleons have a spin of ½ and are the least massive baryons. The nucleons are shown in the table below along with one possible spin state of their constituent quarks.

The other five families of baryons are each named after one of five Greek letters. Delta (Δ) baryons are also made of only up and down quarks, but have a spin of 3/2 because all their constituent quarks are spin-aligned. There are four delta particles as shown in the table. All four have a mass of 1232 MeV/c2. The Δ++ consists of three up quarks and has a charge of +2. The Δ+ consists of two up quarks and one down quark (like the proton) and therefore has a charge of +1. The neutral delta (Δ0) has one up quark and two down quarks (like the neutron) and has a charge of 0. The Δ– consists of three down quarks and has a charge of negative one.

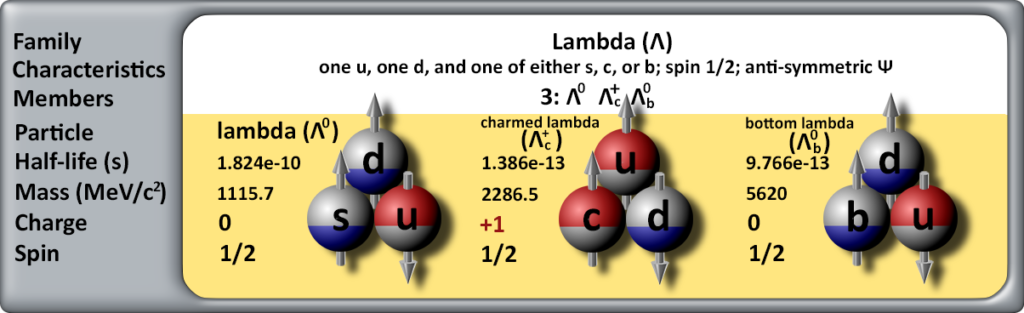
The lambda baryons contain one up quark, one down quark, and one of the heavier quarks (strange, charm, or bottom). These also have a spin of one-half since one quark is always anti-aligned with the other two. But they are heavier than the nucleons because one of their constituent quarks is heavier. There are three lambda baryons as shown below.
The three remaining families are the Sigma, the Xi, and the Omega. These families include some of the heavier quarks. Each of these families contains many members, so we show only one member of each family in the table below. There are 18 members of the sigma family. Each has two of the light quarks (up or down) and one heavier quark. The Xi (also called cascade) baryons contain only one of the light quarks (either the up or down), and two heavier quarks. The omega baryons contain only heavier quarks, and no up or down quarks. Note that no baryons contain any top quarks. Although top quarks can form in high-energy collisions in close proximity to other quarks, the top quark decays so quickly that it cannot settle into a distinct baryon.

These tables depict only the ground state members with one possible spin configuration for the quarks. In addition to spin states of the quarks, the quarks can also revolve around each other, which produces additional spin for the baryon in integer units. This is just like electrons existing in an excited state in an atom. These excited nuclear states result in additional mass due to additional energy. Also, this orbital motion can either increase (if aligned) or decrease (if anti-aligned) the spin of the baryon by integer values. For example, excited delta baryons can have spins of 5/2, 7/2, 9/2, 11/2, and so on. They can also have a spin of ½ if the angular momentum of quark motions is opposite their spin direction. Excited states tend to be very short-lived, and quickly decay.
Baryon Stability
Some people may wonder why they have only heard about protons and neutrons, and not the plethora of other baryons. The reason is that all the other baryons exist for only a fraction of a millisecond before they decay – they spontaneously transform into other particles. Just as the heavier leptons (the muon and tau) decay into other particles, so do most baryons.
However, all the conservation laws must be followed. These laws constrain what types of decay are possible. For example, the total charge of all daughter products must match the charge of the parent baryon because charge is conserved. The lepton number must match. (Baryons have a lepton number of zero. So, if they produce a lepton in a decay, they must also produce an anti-lepton.) The total energy is conserved – which means baryons can only decay into less massive particles (with the kinetic energy of the daughter particles carrying away the difference in mass).
In addition to the conservation laws we covered in the article on leptons, there is also the conservation of baryon number. Baryon number is just what you think it is: the number of baryons. Each baryon has a baryon number of 1. An antibaryon (made of three antiquarks) would have a baryon number of -1. Quarks have a baryon number of 1/3, and antiquarks have a baryon number of -1/3. All other particles have a baryon number of zero.
One implication of the conservation of baryon number is that when a baryon decays, at least one of the particles it decays into will also be a baryon. And since heavier baryons can only decay into lighter ones, it follows logically that the lightest baryon cannot decay. The lightest baryon is the proton with a mass of 938.272 MeV/c2. And indeed, protons are stable. They will not spontaneously decay into anything else.
In fact, all baryons except the proton are unstable. They will decay into lighter baryons, producing other particles in the process to conserve energy, spin state, and charge. The heavier baryons tend to have the fastest decays. This is due mainly to the short lifetimes of the bottom and charm quarks, and to some extent the strange quark. It may be surprising to learn that even neutrons are (slightly) unstable. Neutrons have a mass of 939.565 MeV/c2 – just slightly more massive than the proton. Therefore, they can decay. An isolated neutron will decay into a proton, an electron, and an electron antineutrino. (You can check to see that this indeed conserves electric charge, lepton number, electron number, and baryon number. And the combined mass of the daughter products is less than the mass of the neutron.) The neutron has an average lifespan of about 15 minutes.[6]
Nuclear Stability
But if neutrons only last 15 minutes, then how can atoms exist? After all, every atom except hydrogen has some neutrons in it. These neutrons are essential to hold the protons together. So, how can atoms last longer than 15 minutes? When neutrons are bound by the residual strong force to another baryon, this can have a stabilizing effect due to the negative binding energy. That is, the energy/mass of the system is actually lower if the neutron remains a neutron than if it were to decay into a proton. Conservation of energy therefore prevents decay. Let’s look at one example.
Deuterium is an isotope of hydrogen in which the nucleus consists of one proton and one neutron. This nucleus has a mass of 1875.6 MeV/c2. That neutron might want to decay into a proton, but this would result in a diproton – two protons bound by the residual strong force. However, the diproton has a mass of 1877.8 MeV/c2. The diproton is slightly heavier than the deuterium nucleus because the energy of the bond differs, resulting in a higher energy/mass state. Thus, the neutron in the deuterium nucleus cannot decay because it would result in a heavier particle – and that would violate conservation of energy. So, in this case, the combination of the proton and neutron is stable, whereas the diproton is unstable.
There are many configurations in which the nuclear binding energy can have a stabilizing effect on the neutron. Certain combinations of protons and neutrons in a nucleus are stable because any change would result in a higher energy (more massive) nucleus. And that would violate conservation of energy. This is why the lighter atoms tend to have an approximately equal number of protons and neutrons. For heavier atoms, the neutrons tend to outnumber the protons in order to result in a stable nucleus. In fact, if the neutron-to-proton ratio in an atom is too small, one of the protons will decay into a neutron.[7] So even particles that are normally stable can become unstable depending on their binding energy with other particles.
But one rule is always followed: a nucleus can only spontaneously decay into a less massive nucleus. That will determine whether a neutron can decay, whether a proton can decay, or neither. And the mass of the nucleus depends not only on its protons and neutrons, but also on the binding energy between them. We might ask, “Can X decay into Y?” If Y is heavier than X, then answer is “no.” If Y is lighter than X, then the answer is “possibly – if no conservation laws are violated.”
A Designed Cosmos
One implication of all this is that the mass of baryons and therefore their constituent quarks is not arbitrary. There is a reason why the Lord made the down quark slightly heavier than the up quark. If it were the reverse, if God had made the down quark slightly lighter than the up quark, then the neutron would be slightly lighter than the proton. In that event, isolated neutrons would be stable, but unbound protons would not. Protons would spontaneously decay into neutrons.[8]
But hydrogen gas has a nucleus of one proton.[9] Thus, ordinary hydrogen gas could not exist if the down quark were slightly lighter than the up quark. And 90% of the matter in the universe is hydrogen gas. It is what stars are made of and is their source of power.[10] Furthermore, water molecules consist of two parts hydrogen to one part oxygen – and water is essential for life. Making the down quark slightly heavier than the up quark is therefore a design feature.
Conversely, if the Lord had made the down quark significantly heavier than it is, then the nuclear binding energy would be insufficient to prevent all neutrons in all atoms from decaying because the result would always be less massive. Yet, the neutrons are what prevent the nucleus in heavier atoms from splitting. So, the only atom that could exist would be hydrogen, and life would not be possible. Again, we see the incredible intelligence that went into designing quantum particles and the rules that govern their behavior.
A Problem for the Big Bang
Since baryon number is conserved in any collision or decay of particles, the baryon number before the event must match the baryon number after the event. Thus, if any new baryons are created, an exactly equal number of antibaryons must also be created. This is a problem for big bang supporters because in their view the universe started in a high-energy state with no baryons. Yet, today, we estimate there are roughly 1080 baryons in the visible universe. The number of antibaryons is essentially zero compared to that since antibaryons are only produced in high-energy situations and almost instantly destroyed upon contact with matter. But if our universe once had no baryons (as the big bang requires), then there should be an equal number of baryons and anti-baryons today, since they are only naturally produced in equal numbers. There should be an equal amount of matter and antimatter. But there isn’t. Our universe is essentially matter only. The big bang story violates conservation of baryon number. And it violates it by an enormous amount. This is known as the baryon asymmetry problem.
Of course, this is a feature for creation. The creation of the universe was not a natural event. God is not bound by the laws He imposes on nature today. He was free to create baryons without creating any antibaryons. Of course, the Lord had a good purpose for this. When baryons contact antibaryons, they destroy each other and release enormous energy. We could not exist in such a universe.
Balance in the Cosmos
Also, consider that the number of charged leptons in the universe precisely matches the number of charged baryons, at least within our ability to measure them. That is, as far as we can tell, there are exactly as many electrons in the universe as protons. Therefore, the number of negative charges balances the number of positive charges, resulting in a universe that is exactly electrically neutral on large scales.
This is an important design feature. What if the universe had just 1% more negative charge than positive charge? That is, what if for every 100 protons there were 101 electrons? In that event, the universe would have a net electrical charge of -1 per 100 atoms. Everything in the universe would electrically repel everything else in the universe. And since the electric force is much stronger than the force of gravity, planets and stars could not exist. Their inward pull of gravity would be unable to overcome the outward force of electrostatic repulsion.
It’s pretty amazing what the Lord made out of primarily just two varieties of quarks along with electrons. The situation becomes even more fascinating when we consider that quarks can bind to antiquarks into particles called mesons. Mesons are important because they are involved in the residual strong force. Without mesons, matter could not exist. More to come.
[1] This is a simplified explanation. I am of course referring to valence quarks and not “sea quarks.”
[2] This does not include excited states in which quark motions contribute to spin – to be discussed later.
[3] Although this is true in chemistry as well, the difference there is normally too small to measure. Yet, a hydrogen atom is slightly less massive than the mass of its electron and proton (if they were widely separated).
[4] We now know that gluons also contribute to the spin state. But this detail is beyond the scope of this article.
[5] You may wonder why there are no nucleons with three up quarks or three down quarks. However, these cannot exist because of the Generalized Pauli Principle. This principle gives additional rules for what spin states are allowed. For example, if all three quarks are the same flavor, then they must also be spin-aligned (as in Delta baryons). But nucleons by definition have one quark anti-aligned with the other two. Three quarks of the same flavor do exist in delta baryons, because they are spin-aligned.
[6] Average lifetime is related to (but is not the same as) the half-life. The half-life is given by the natural logarithm of 2, multiplied by the average lifetime. The neutron has a half-life of 10.4 minutes.
[7] This can occur by electron capture in which one of the electrons is absorbed by a proton to become a neutron. An electron neutrino must also be released to conserve lepton number. As one example, Aluminum-26 is radioactive and can decay into Magnesium-26 by electron capture.
[8] Either by electron capture or positron emission.
[9] The most common isotope of hydrogen by far has exactly one proton. Less than 0.02% of hydrogen is deuterium, which has one proton and one neutron.
[10] Perhaps deuterium could exist in such a scenario. But deuterium undergoes fusion at a much lower temperature than hydrogen-1. Thus, stars would have to be much smaller and less massive to compensate, which would change the orbital period of planets, and so on. Whether life would be possible in such a situation is known only to the Lord.