In the previous article we explored some of the basic properties of quantum particles, including the electron. But the electron is merely one member of a group of particles called leptons. The term lepton comes from the Greek and means “small,” or “thin” and refers to the extremely low mass of leptons.[1] The electron, for example, is 1800 times less massive than a proton.
Classification of Leptons
There are exactly six types (called “flavors”) of leptons. Three of these are charged leptons; they have an electric charge of -1 just like the electron. The three charged leptons are the electron (e–), the muon (μ–), and the tau (τ–). These are referred to as the three generations of charged leptons. Muons were discovered in 1936, and were originally misclassified as mesons (to be discussed in a later article). For this reason, older literature might refer to muons as mu-mesons. But we now know that muons are leptons, and essentially heavier versions of electrons. The muon is 207 times heavier than the electron, but is otherwise identical. The tau, discovered in the 1970s, is 3477 times the mass of an electron. This means the tau is almost twice the mass of a proton, and is the only “heavy” lepton.

The other three leptons are electrically neutral and are called neutrinos – designated by the Greek letter nu (ν). Each of the three neutrinos is basically an uncharged version of one of the three charged leptons. So, there is an electron neutrino (νe), a muon neutrino (νμ), and a tau neutrino (ντ). All three generations of neutrinos are extremely low mass. In fact, for many years, the electron neutrino was thought to be massless. But we now have evidence that it has a tiny amount of mass.[2] Nonetheless, the mass of neutrinos is currently smaller than our ability to detect experimentally, something like a million times smaller than the mass of an electron.
We would expect the charged leptons to be far more massive than the neutral versions. When two particles are both negatively charged (or both positively charged), they repel each other. Thus, it takes energy to push like charges together. Imagine a cloud of negative charge, and then push it into the tiny volume of an electron. [3] This would take energy. Thus, electrons have potential energy because they contain self-repelling charge compressed into a small volume. Einstein discovered that energy has mass. And since electrons have internal potential energy due to their self-repelling charge, they have mass. Neutrinos do not have the internal energy of charge, and therefore are much less massive than any of the charged leptons.[4]
The Ghostly Nature of Neutrinos
The sun is a strong source of neutrinos. In the solar core, hydrogen undergoes nuclear fusion to become helium. One of the byproducts of this process is neutrinos. One fascinating aspect of neutrinos is their ghostly ability to pass through ordinary matter. They stream away from the core of the sun, passing effortlessly through its bulk and into space. Right now, about 100 trillion neutrinos are passing harmlessly through your body every second! These are the very neutrinos produced by the sun. This continues even at night when the sun is below the horizon; the neutrinos pass through the earth first and then through your body and into space.
The reason neutrinos can pass through matter is because matter is mostly empty space. The nucleus of an atom is tiny compared to the size of the atom. The electrons orbit at distances roughly ten thousand times the size of the nucleus. Since an atom is mostly empty space, a neutrino could only be stopped if it is unlikely enough to collide directly with the nucleus or with one of the electrons. But the probability of that happening is infinitesimal. In fact, a neutrino can pass through roughly 6 trillion miles of solid lead before it is likely to impact an electron or nucleus! This ghostly property of neutrinos makes them very difficult to detect. Consequently, neutrino detectors can observe only the tiniest fraction of neutrinos that pass through them.
Given that atoms are mostly empty space, it makes sense that neutrinos can pass through atoms undeterred. The question then becomes, why don’t other particles do this too? The answer is that many other particles are either charged, contain charged particles, or otherwise interact with the intense electric field within an atom. The atom itself is made of a positively charged nucleus and a negatively charged electron cloud. So, any charged particle that comes near an atom is strongly affected by the electric force of that atom. This is why atoms collide with each other; their electron clouds are mutually repulsive.
Spin
Elementary particles also have a property called “spin.” This is because they behave mathematically as if they were rotating.[5] No external torque is causing this rotation; particles are simply born “spinning.” Nothing can affect the rate of their spin either. It is simply a property of the particle.
The electron, for example, has a small magnetic moment – meaning it acts like a little magnet. Magnetic moments are produced by rotating a charged object. So, the electron behaves somewhat like a little charged rotating sphere. On the other hand, the electron has no apparent size. So how can it rotate? This is part of the weirdness of quantum physics.
It’s best to think of spin as built-in angular momentum of certain elementary particles. Spin is quantized into integer or half-integer units. That is, particles come with a spin of 0, ½, 1, 3/2, 2, 5/2, 3, and so on. All leptons have a spin of ½. So do protons and neutrons.[6] All photons have a spin of 1.
Although we cannot affect the rate of spin, we can affect the direction of spin. Imagine looking down on top of a spinning ball that is rotating clockwise. Now take that spinning ball and flip it upside down. It will now appear to be spinning counter-clockwise. Likewise, the spin of electrons can be flipped upside down. So, when we measure the spin state of an electron, it will either be +½, or -½. Thus, we say electrons are either “spin-up” (+½) or “spin-down” (-½). But the magnitude of their spin is always exactly one half.[7]

You might think we could turn an electron on its “side” so that the spin is neither up nor down. However, measured spin states are quantized. A detector will always find a spin-½ particle to be either spin-up or spin-down. No measurable in-between states are allowed.
Fermions and Bosons
Particles that have half-integer spins (such as ½ or 3/2) are called fermions. This is in honor of Enrico Fermi, who along with Paul Dirac discovered the way large sets of fermions behave. Fermions obey a law of nature called the Pauli exclusion principle. Named after its discoverer, Wolfgang Pauli, this principle states that no two fermions can occupy the same quantum state at the same time. Basically, this means that you cannot put two fermions of identical spin states into a given location with the same energy.
The Pauli exclusion principle, along with the fact that electrons are fermions, is responsible for atomic structure. For example, how many electrons can occupy the ground state (the lowest energy level) in an atom? The answer is two – if one is spin-up and the other is spin-down. You cannot place a third electron in the ground state because it would have the same spin, energy, and momentum of one of the other two electrons – the same quantum state. Thus, a third electron in an atom must exist in a higher energy level than the ground state. This is why atoms have quantized electron shells.
Particles that have integer spins (such as 0, 1, 2) are called bosons. This is in honor of Satyendra Bose who along with Albert Einstein discovered the way large groups of bosons behave. One of the main differences between bosons and fermions is that bosons are not constrained by the Pauli Exclusion principle. You can put as many bosons as you like into the same quantum state. Photons, particles of light, are bosons. Multiple photons can exist in the same place at the same time. In fact, that is what a laser is. A laser beam is a form of light in which many photons exist in the same quantum state.
Making Matter
Suppose that God had given electrons a spin of 1 instead of ½. In that event, electrons would be bosons rather than fermions, and would ignore the Pauli exclusion principle. All electrons in all atoms would fall into the ground state. All atoms would behave somewhat like heavier versions of hydrogen, chemistry would not exist, and biological life would not be possible.
On the other hand, suppose God had given electrons a spin of 3/2. The possible spin states for a 3/2-spin particle are 3/2, ½, -1/2, and -3/2. Thus, we could place four electrons rather than two into the ground state of any atom. Consequently, all of chemistry would change. Beryllium, for example, would be inert like helium is now. Whether biological life would be possible with that alternate chemistry is known only to God.
Antimatter
In 1928, physicist Paul Dirac showed that the equation governing electrons had two possible solutions. That is, the equation showed that electrons could have either negative or positive charge. Essentially, this showed that in addition to electrons, the universe could also contain anti-electrons (also called positrons) which were identical in every way to electrons except with a positive charge. The positron was definitively detected in 1932. The positron was the first predicted, and first discovered particle of antimatter: a particle having the opposite charge of a known particle, but which is otherwise identical.
We now know that all particles have an antimatter counterpart. Just as there are positively charged protons, there are negatively charged anti-protons. Just as there are muons and tau particles, there are also anti-muons and anti-tau particles. Theoretically, there could be antimatter atoms such as anti-hydrogen in which a positron orbits an anti-proton.
Some neutral particles are their own anti-particle. For example, photons and anti-photons are identical. Yet, other neutral particles are different from their antimatter counterpart. Neutrons are different from anti-neutrons because neutrons are made of quarks and anti-neutrons are made of anti-quarks.[8]
Fortunately, antimatter particles tend to be scarce. That is, there are far more protons and electrons in the universe than anti-protons and positrons. Why is this fortunate? When particles of matter touch their antimatter counterpart, they destroy each other and release energy such as photons.[9] If the universe were equal parts matter and antimatter, we would not be here to discuss it. Since the universe is dominated by matter, most antimatter particles have only a fleeting existence. They are created in high-energy particle collisions, only to be almost immediately destroyed when they inevitably interact with ordinary matter. The lack of abundant antimatter is a problem in the big bang story, as will be discussed in a later article.
Particle Transformations
Quantum particles have the capacity to change into other particles under certain circumstances. Some will do this spontaneously; they will simply change into some other combination of particles. The spontaneous transformation of one particle into another is called “decay.” Particles that decay into other particles are called “unstable.” We will find that the overwhelming majority of quantum particles are unstable. They have only a fleeting existence, lasting less than a microsecond, before they transform into something else. Particles that do not spontaneously transform into others are called “stable.”
Electrons are stable. This is important because the electron structure is what determines the chemical properties of atoms. If electrons were unstable, then the chemical properties of matter would not be constant and biological life would not be possible.
Muons and tauons are unstable. In fact, they are very unstable. Muons have a typical lifetime of 2.197 microseconds. The tau is even more unstable; it lasts only 2.903×10-13 seconds. Neutrinos are stable, although we now know that they oscillate (they can change between the three flavors).
In many circumstances, we can actually predict which particles are unstable, and what kind of particles they decay into. This is because there are certain conservation principles that all particle transformations must obey. For example, there is the law of conservation of energy. This law requires that the total energy of all particles before a transformation must equal the total energy of all particles after the transformation. This includes the mass of all the particles since mass is a type of potential energy. One implication of the law of conservation of energy is that massive particles tend to decay into less massive particles that carry away some of the energy in the form of motion. Generally, the more massive a particle is, the faster it decays.
Another conserved quantity is electric charge. The total charge of all particles before the interaction must be the same as the total charge after the interaction. So, a muon cannot decay into a single positron, because the charge before the transformation (-1) would not match the charge after (+1).
Total momentum is also conserved. Momentum is the product of mass and velocity. The momentum of a particle before its decay must exactly match the sum of the momentum of all particles after the decay.
Spin state is also conserved. The total added spin states of all the particles before and after the transformation must match. Remember, spin states can be positive or negative. So, a spin +½ particle could decay into two particles: a particle with spin -½ AND a particle with spin +1. Or it could decay into three particles with spin states, +½, +½, and -½. Other possibilities exist.
Lepton number is also conserved. Lepton number simply refers to the number of leptons present. So, an electron has a lepton number of 1. So does a muon, a tau, and each of the three flavors of neutrinos. Anti-leptons have negative lepton numbers. So, a positron has a lepton number of -1. All non-leptons have a lepton number of zero.
There are also some quasi-conserved quantities; these are conserved in most transformations, but not all. Electron number, muon number, and tau number are quasi-conserved. Electrons and electron-neutrinos each have an electron number of one. Likewise, muons and muon-neutrinos have a muon number of one, etc. Anti-muons and muon anti-neutrinos have a muon number of -1 just as we would expect.
Generally, if a massive particle can decay into less massive particles without violating any of the above rules, it will. Hence, we can predict which particles are stable, and which are unstable. We can also predict some of the possible daughter particles using the conservation rules.
Lepton Decay
With these rules in place, we can deduce which leptons decay and how. For example, a muon decays into three particles: an electron, an electron anti-neutrino, and a muon neutrino. The total mass of these three particles is less than the mass of the muon. So, energy is conserved (the kinetic energy of the resulting particles carries away the difference in total mass). Charge is conserved because the total charge before and after is -1. Spin state is conserved; if the muon is spin up (+½) then the three spin-½ particles could be +½, +½, and -½ which sums to ½. Lepton number is conserved because the anti-neutrino has a lepton number of -1, which when added to the other two leptons gives a total lepton number of 1. The electron number and muon number are both conserved in this reaction because the electron anti-neutrino has a negative electron number, canceling the electron. And the muon-neutrino has a muon number of 1.

What about the tau? Since it is very massive, it decays very quickly. And since there are many particles less massive than the tau, there are many different ways it can decay. One possibility is for the tau to decay into an electron, an electron anti-neutrino, and a tau neutrino. You can see that this reaction conserves energy, charge, spin state, lepton number, etc. Another possibility is that the tau will decay into a muon, a muon anti-neutrino, and a tau neutrino. This likewise obeys all the conservation laws. Of course, the muon will then decay into an electron, an electron anti-neutrino, and a muon neutrino. Since there are several other types of particles less massive than the tau (which we have not yet discussed), several other decay pathways are possible. But in all cases the conservation laws are always followed.
We can also see why the electron must be stable. The electron cannot decay into any combination of neutrinos because charge would not be conserved. Any electron decay must result in a total charge of all particles that equals -1. But there are no charged particles less massive than the electron. Hence, it cannot decay.
Also, neutrinos cannot decay.[10] We might at first think that they could decay into photons, since photons are massless and have no charge. But this would violate conservation of lepton number. Also, no combination of photons can produce a +½ or -½ spin state, since photons are bosons.
Although particles can only naturally decay into less-massive particles, it is possible to force a reaction to go the other way by supplying large amounts of energy. This is how particle accelerators work – like those at CERN or Fermilab. They accelerate particles up to a high fraction of the speed of light in opposite directions, and allow them to collide. If the kinetic energy in such collisions is greater than the mass of a particle, a particle can be produced. The types of particles produced are governed by the above conservation laws.
For example, only particles of less or equal mass to the energy of the collision can be produced. This is why more powerful particle accelerators can produce more massive particles. Also, the change in net charge must be zero, and lepton number and total spin state are also conserved. Therefore, if an electron is created in such a collision, an anti-electron (positron) will also be produced. Energy from particle collisions always results in the production of an exactly equal amount of matter and antimatter.
The existence of the neutrino was predicted on the basis of the above conservation laws. Physicists had discovered that neutrons can decay into a proton and an electron. But the total energy of the proton and electron was always somewhat less than the total energy of the neutron. And the total momentum was apparently not conserved either. In 1930, Wolfgang Pauli proposed that there must be a third particle produced which carried away the extra energy and momentum. This particle would have to be neutral in order for charge to be conserved. And it would have to be very low mass since in some cases only a small amount of energy was “missing.” As such, it would be a neutrino – Italian for “little neutral one.”
The ghostly nature of the neutrino makes it extremely difficult to detect. Pauli once whimsically stated, “I have done a terrible thing, I have postulated a particle that cannot be detected.” It took two and a half decades, but the neutrino was definitively detected in 1956.
Quantum Astronomy
One interesting quantum interaction that is very relevant in astronomy involves the electron in the ground state of a hydrogen atom. The proton of a hydrogen atom is a fermion with a ½ spin. It can therefore be either spin-up (+½) or spin-down (-½). The electron circling that proton is also spin ½, and can be either spin-up or spin-down. If the two spins are in the same direction (both spin-up or both spin-down), the energy state of the electron is slightly higher than it would be if the spin states were opposite.[11] Therefore, it is possible for a hydrogen atom with aligned spin states to “decay” into a hydrogen atom with opposite spin states.
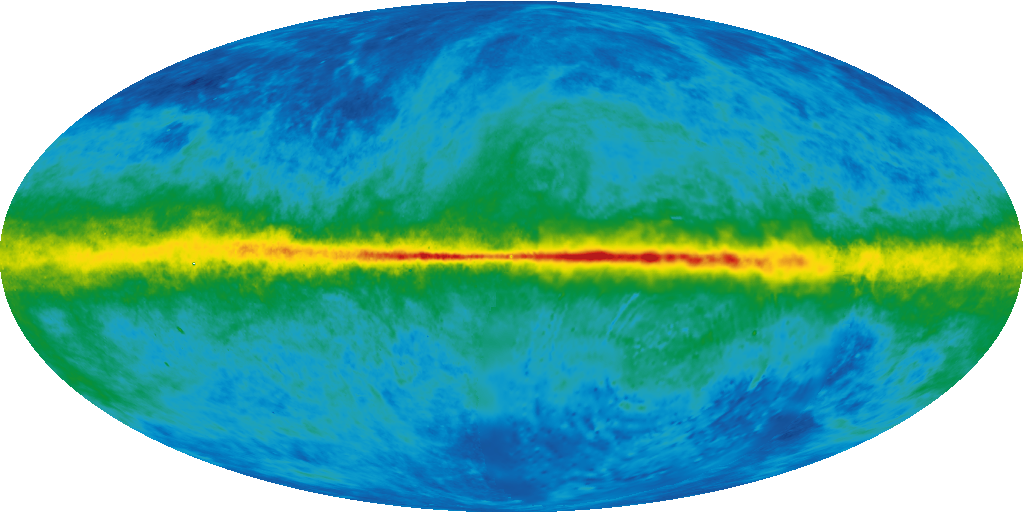
The energy difference between the two states is only 5.9×10-6 eV. The electron can flip its spin state – but only by obeying all the conservation rules. It must release exactly 5.9×10-6 eV of energy. The only discovered particle with less mass than 5.9×10-6 eV is the photon[12]. Furthermore, the total spin of the system has gone from 1 to zero. Therefore, it must release a particle with a spin of 1. Photons have a spin of 1. Sure enough, the hydrogen atom can drop from the aligned spin-state to the slightly lower energy (anti-aligned) state by releasing a photon with energy 5.9×10-6 eV, which corresponds to a wavelength of 21 cm. This is in the radio region of the electromagnetic spectrum. Astronomers use radio telescopes to detect this 21 cm line, and map the structure of the Milky Way galaxy. Our galaxy “glows” in 21 cm radio waves because the electrons in its hydrogen atoms are constantly flipping from aligned to anti-aligned spin states.
Particles Common and Exotic
Of the six leptons, the only one most people directly experience are electrons. Electricity is due to the flow of electrons, and we are all familiar with electricity. The muon and tau particle have such a fleeting existence that it takes specialized equipment to detect them. And although the three flavors of neutrinos are constantly passing through our bodies every second, they are invisible and rarely interact with ordinary matter.
Likewise, we have some familiarity with protons and neutrons, because we are made of them. These are primarily responsible for our mass. But they are merely two examples of a class of particles that contains many others. More to come.
[1] Five of the six types of leptons are very low mass. The heaviest lepton, the tau, had not yet been discovered when the term ‘lepton’ was coined.
[2] The discovery that neutrinos oscillate between flavors demonstrates that they have finite rest mass. Physicists have demonstrated mathematically that massless neutrinos would not oscillate.
[3] Although we might think of an electron as a tiny sphere, it often behaves as if it had no size at all (like all elementary particles). This is just another example of the counterintuitive nature of quantum physics.
[4] The reason neutrinos have any mass at all is currently disputed because there is more than one possible mechanism.
[5] The only known (elementary) exception is the Higgs boson which has a spin of zero.
[6] In some sense, you can think of higher spin numbers as rotating faster (they correspond to higher angular momentum). But there is more to it than that; the spin also describes how objects behave under rotation. Particles with spin 1 act somewhat like we would expect. If you rotate a spin-1 particle by 360 degrees, it will return to its original state. However, if you rotate a spin-½ particle by 360 degrees, you get a reversed version of the original. You must rotate a spin-½ particle by 720 degrees to return it to its original state. On the other hand, a spin-2 particle needs to be rotated only 180 degrees to return to its original state.
[7] Spin states are quantized too. For a given particle, its spin states are separated by integer values up to the spin of the particle, or down to the negative of its spin. So, a particle of spin 1 could have a spin state of -1,0, or, +1. A particle of spin 3/2 could have a spin state of -3/2, -1/2, 1/2, or 3/2. An exception to this rule exists for particles with no rest mass; they have only two spin states – the positive or negative of their total spin. Thus, photons can have a spin state of either 1 or -1.
[8] Presently, we do not know if neutrinos are their own anti-particle. This is an unsolved problem in modern physics. We will proceed in this article series as if neutrinos are distinct from anti-neutrinos.
[9] Photons (and anti-photons) themselves are exempt from this pattern since they are already photons.
[10] Neutrinos do oscillate – meaning they can switch from one flavor to another. But this is not a decay in the traditional sense. Rather it has to do with the three overlapping wavefunctions that propagate at different speeds, making the probability of detecting a particular flavor of neutrino a function of energy and distance.
[11] This is due to the magnetic moments of the proton and electron respectively. The electron flipping its spin is much like pushing two bar magnets together (north to north), and one of them flips around.
[12] The as-yet-undiscovered graviton must also have a rest mass of zero – like the photon. However, the graviton has a spin of 2, and therefore cannot be emitted as a result of an electron flipping spin state.