It is rather amazing what we can know about stars simply by analyzing their light and with rigorous application of logic and mathematics. We can measure the distance to any nearby star using parallax. And by multiplying a star’s apparent brightness by the square of its distance, we can determine its actual luminosity. Furthermore, we can know both the composition and the surface temperature of a star by analyzing the absorption lines of its starlight using a spectroscope. This led to the field of stellar classification and the discovery of the main sequence. But why does this sequence exist? Why are blue main sequence stars so much brighter than red main sequence stars?
The Luminosity-Temperature Relation
In the late 1800s, Josef Stefan and Ludwig Boltzmann independently demonstrated that the energy radiated by a hot object of a given size is proportional to the fourth power of the object’s temperature. So, if you heat up a substance, it will glow. If you double its temperature (in Kelvins), the object will glow sixteen times brighter! This law works regardless of the composition of the substance.
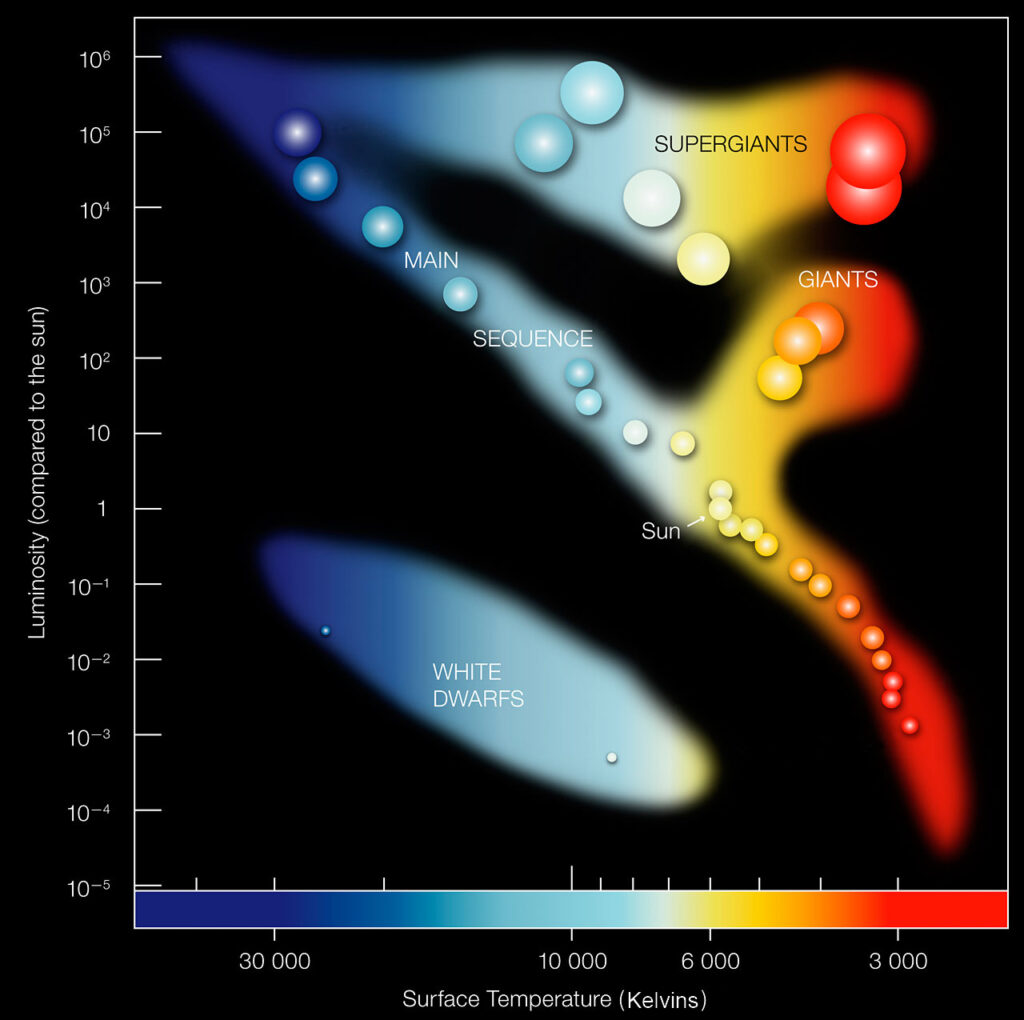
This partially explains the main sequence. Recall that when stars are plotted on an H-R diagram in which luminosity is the y-coordinate and temperature class is the x-coordinate (with temperature decreasing with x), most stars fall along a natural curve – the main sequence. In this curve, the blue stars are far more luminous than the red stars. We now partly understand why: the blue stars shine brighter than the red ones because they are hotter. But that’s not the full answer. Since luminosity is proportional to the fourth power of temperature, we expect a blue star with a temperature of 30,000 Kelvins will shine 10,000 times brighter than a red star of the same size at 3,000 Kelvins. Yet, blue stars shine even brighter than this. Why?
The resolution is found in the phrase “of the same size.” An object of a given size will give off energy proportional to the fourth power of temperature. But increasing the size of the light-emitting substance will also increase brightness. It makes sense that if you have more light-producing elements over a larger area, you will have more light. So, brightness is proportional to the surface area of the light-producing substance. This is also true of stars.If you wanted to make a star shine brighter, there are two ways to do it. One way is to increase the surface temperature of the star. But another way is to increase the size of the star. Its surface area is proportional to the square of the radius. So, these two effects (temperature and size) combine to determine the luminosity of a star. Thus, if star A is brighter than star B, star A must either be (A) physically larger than star B, (B) hotter than star B, or (C) both.[1]
The main sequence has a steeper slope than it would have if stellar luminosities were only due to temperature differences in stars that are all the same size. Therefore, we conclude that blue main sequence stars must have a larger diameter than yellow main sequence stars, which are larger than red main sequence stars. Furthermore, in order for the main sequence to be as narrow as it is, a star of a given temperature class must be approximately the same size as any other main sequence star of the same temperature. For example, the sun is class G2. Other G2 main sequence stars will be roughly the same size as the sun. On the other hand, a G2 star will always be larger than, say, an M3 main sequence star.
A Mass Sequence
But what causes main sequence stars of the same temperature as the sun to be about the same size? The answer is mass. Most stars are part of a binary system in which two or more stars orbit their common center of mass. By measuring their orbital period and their distance from each other, we can compute the mass of the stars from Newton’s laws. From such studies, we know that main sequence stars with about the same mass as the sun also have about the same size and temperature. Main sequence stars more massive than the sun are hotter, bluer, and more luminous than the sun. And stars that are less massive than the sun are cooler, redder, and smaller. The main sequence is therefore a mass sequence. The stars on the upper left of the main sequence are more massive than the stars on the lower right. In fact, if you know a star’s mass, you can plot its approximate position on the main sequence.
We now understand the mechanism by which this effect is produced: nuclear fusion in a star’s core. We saw previously that all stars are composed of hydrogen and helium gas. The mass of all the gas creates a gravitational force that attempts to compress the star into a point. However, the outward force of gas pressure tends to prevent such a collapse. In a normal main sequence star, the inward force of gravity and outward force of gas pressure are exactly balanced. (If they weren’t, then the star would either expand or shrink until the two forces match.) The pressure and temperature in the core are so great that hydrogen nuclei are slammed together to form helium. The net reaction is that four hydrogen atoms eventually become one helium atom, which releases an enormous about of energy.
A low-mass star has less gravity, and so the pressure in the core is somewhat less than in heavier stars. This results in less fusion, meaning less energy is produced. The star will be fainter and have a lower surface temperature than a heavier star. The star will be smaller because it has less mass and less gas pressure. Conversely, a high-mass star will have greater pressure and higher temperature in the core. This results in greater fusion and higher energy output. The star will be hotter and more luminous. It will also have a larger diameter because it has more gas and the outward pressure is higher. From computer simulations we can show that a star of a given mass will indeed reach an equilibrium condition in which core fusion produces the energy necessary for the star to be the size, temperature, and luminosity of a main sequence star. We conclude that main sequence stars are powered by fusion of hydrogen into helium. This process produces subatomic particles called neutrinos which stream away from the stellar core. We have indeed detected neutrinos from the sun, confirming that it is powered by nuclear fusion.
Non-Main Sequence Stars
The majority of stars in our galaxy (around 90%) fall on the main sequence. So, if you know the mass of the star, you can immediately know its luminosity, surface temperature, and approximate diameter – if it’s on the main sequence. But around 10% of stars do not fall on the main sequence. They are above it on the H-R diagram. What can we conclude about these stars? Consider a G2 star of the same temperature as the sun but which lies above the sun on the H-R diagram, meaning it is brighter than the sun. One star can be brighter than another if (A) it is hotter, (B) it is physically larger, or (C) both. But since this G2 star has the same temperature as the sun, it cannot be hotter. We must conclude that it is larger. Thus, stars not only have a temperature class but a size/luminosity class as well.
Astronomers classify a star into one of (roughly) five size/luminosity bins. Main sequence stars are the smallest and are assigned class 5 with the Roman numeral V. Standard notation is to place this after the temperature class. So, the sun is a G2V star. Since main sequence stars are the smallest type, they are referred to as dwarf stars. Sometimes the temperature/color class is included (e.g., “blue dwarf”). Thus, the sun can be said to be a yellow dwarf. Proxima Centauri is a red dwarf because its class is M5V. There is one exception: white main sequence stars must not be called “white dwarfs” because this term is reserved for another type of object.[2]
Stars somewhat larger than main sequence stars are called sub giants and are class IV. Giant stars are class III. Class II stars are called bright giants. The largest stars are class I and are called supergiants. For increased precision, the supergiant class is further divided into Ib (smaller) and Ia (the very largest and brightest stars).
It is important to note that this notation (Ia, Ib, II, III, IV, V) reflects only the relative size and luminosity within a temperature class. In other words, a B9III star will definitely be both larger and brighter than a B9V star. But you cannot assume that an O9Ib star will be larger than a K5III star. In fact, a blue supergiant can be smaller than a red giant.
Blue stars have the least range of size. All blue stars are larger than the sun, but the brightest blue supergiants would be only 50 times the diameter of the sun. Conversely, red stars have the greatest range in sizes. A main sequence red star will be smaller than the sun, but the red supergiant Antares is over 700 suns in diameter. Thus, the smallest stars in the universe are red, and the largest stars in the universe are also red.
Red dwarfs are the most common type of star. Of the fifty nearest stars, all are main sequence, thirty-nine are type-M and six are type K, for a total of forty-five red dwarfs! Of the remaining stars, three are type G (including the sun), one is type F, and one is type A. So, red stars far outnumber all others. Yet, our night sky does not appear to be filled with red dwarfs. That is because they are the faintest class and are very difficult to see. On the other hand, the one type A star in the list is Sirius – the brightest star in our nighttime sky. We tend to see more of the white and blue stars, not because they are common, but because they are exceptionally bright.[3]

The three brightest stars comprise Orion’s belt. From left to right they are Alnitak, Alnilam, and Mintaka.
Blue O-type stars are extremely rare. Yet, they are easy to detect because they are the brightest class of star. Consider the stars of Orion’s belt which dominate the winter sky. The left star on the belt is Alnitak, class O9Ib. So, it is a blue supergiant, nearly 9,000 times as luminous as the sun. The star on the right is Mintaka which is class O9II. It is a blue bright giant, nearly 5,000 times as luminous as the sun. Since Alnitak and Mintaka are the same temperature class, we can conclude that Mintaka is physically smaller than Alnitak. The middle star of the belt, Alnilam, is type B0Ia, a blue supergiant only slightly cooler than the other two but more luminous. Alnilam is over 60,000 times as luminous as the sun. Since it appears about the same brightness as the other two, you might conclude that it must be farther from us. (And you would be right.)
Speculations on Stellar Aging
What is the cause of these higher size/luminosity classes? We saw that the main sequence is simply the result of stars of various mass fusing hydrogen in their core and being in an equilibrium condition in which outward gas pressure matches the inward force of gravity. It seems reasonable to infer, therefore, that stars of a larger/brighter class are either (A) powered by something other than hydrogen fusion in the core, (B) not in an equilibrium state, or (C) both. Most astronomers believe that the first option is the best. Giant stars may be fusing helium in the core, which requires a higher temperature and pressure than hydrogen fusion. In addition to helium core fusion, they may also be fusing hydrogen in a shell around the core. However, this condition would only happen if there were no hydrogen in the core – only helium.
In principle, if a star like the sun were to exist for a long duration, it would eventually convert all the hydrogen in its core into helium. This would cause the core to collapse, thereby gaining sufficient pressure to initiate a helium flash in which helium begins to fuse into heavier elements. Most astronomers believe that non-main sequence stars are aged stars – those that were once on the main sequence but have departed after exhausting all the hydrogen in their core and have begun helium fusion.
Based on the size of the sun and its energy output, it would theoretically take ten billion years for it to convert all its core hydrogen into helium. However, this assumes that its core composition was initially identical to its surface composition. If the star began its existence with very little hydrogen in the core but lots of helium, it would take much less time to fuse the remaining hydrogen. We don’t know that God created each and every star with a “full tank of gas.” Furthermore, how do we know that God didn’t create some stars with only helium in their core to begin with, in which case they would begin their existence already off the main sequence?
So, secular speculations on stellar evolution are based on a number of untestable assumptions. But observations are lacking. We have never seen a main sequence star become a non-main sequence star. So, claims of stellar evolution should be considered tentative at best.[4] Many secular astronomers are quite confident in their current views on stellar evolution. But then again, they were once confident that blue main sequence stars evolved into red dwarfs – which we now know to be false. The main sequence is not a time sequence, but a mass sequence indicating the equilibrium condition for stars that fuse hydrogen in their core. Non-main sequence stars are apparently doing something else. Creation astronomers continue to research topics of stellar aging.
There are, however, certain kinds of changes in stars that we do observe. Some stars pulsate: they rapidly expand and contract in a periodic way. Some stars will spontaneously brighten by an enormous amount before returning to their standard brightness. And occasionally, a star will simply explode – an event called a supernova. We will explore these in the next article.
[1] With the all the details included, the equation for a star’s luminosity looks like this: L = 4πσr2T4, where σ is the (known) Stefan-Boltzmann constant which has a value of 5.67 × 10-8 W m-2 K-1. There are three variables in this equation: L, r, and T. So, if we know any two variables, we can solve for the third. If a star’s distance is known, then its luminosity can be computed. And the temperature of any star is easy to determine from its spectrum. Thus, we can compute the size (diameter) of any star of known distance.
[2] My apologies to the late J.R.R. Tolkien who was adamant that the plural of “dwarf” is “dwarves.” That is certainly the case in Middle Earth. But in astronomy, main sequence stars are “dwarfs.”
[3] This is an example of a selection bias.
[4] Many astronomers would point to cluster turn-off points as evidence in favor of the standard model of stellar evolution. That is, some star clusters have a deficit of early type main sequence stars but an abundance of giants. Since early type stars exhaust their fuel more quickly than late type stars, they would indeed leave the main sequence sooner. Thus, secular astronomers use this as a tool to estimate the age of the cluster. However, even clusters that are assumed to be very old often contain a handful of blue main sequence stars known as “blue stragglers,” which is contrary to the predictions of the model. Secular astronomers suppose that such stragglers formed by stellar mergers and are therefore recent, but there is no way to test this.