Quantum physics deals with how the universe behaves at very small scales – on the level of atoms and smaller. And it’s weird: very weird. Particles that are smaller than atoms do not behave in exactly the same way as the much larger objects to which we are accustomed. This makes quantum physics one of the most intriguing areas of research, and one which declares the glory and majesty of the Lord.
Atoms
We are taught in school that all matter is made up of very tiny particles called atoms. Some substances consist of only one type of atom – these are called elements. Gold, silver, lead, oxygen, carbon, hydrogen, helium, and aluminum are all examples of elements. The smallest particle of gold, for example, is a single atom. Amazingly, there are only about 90 naturally-occurring elements.
But atoms can also bond with other types of atoms to form a compound. Water is a common example. The smallest particle of water is not a single atom, but a molecule made of two hydrogen atoms bonded to an oxygen atom. All the physical properties of any given substance are completely determined by the atoms that comprise it. And the properties of atoms are determined entirely by their constituent components and the rules of quantum physics.
For example, the fact that water is liquid at room temperature and at standard atmospheric pressure is completely determined by the rules that define how the oxygen atom combines with the hydrogen atoms. It’s all quite complicated, and that’s the point. When God created this universe, He made certain kinds of particles and determined the rules that govern them so that life would be possible. That is a logical computation far beyond the capacity of all human minds combined!
Atoms themselves are composite particles; that is, they are made of smaller particles. One or more electrons swarm around the central nucleus of an atom. The cloud of electrons is what gives an atom its size. The central nucleus consists of one or more protons. Protons are larger and 1800 times more massive than electrons. Protons have a positive electrical charge, and electrons have a negative electrical charge that is equal in magnitude to the proton but opposite in sign. Thus, there is a strong attractive force between the nucleus of an atom and the electrons swirling around it. This force is what keeps the high-speed electrons from escaping. Normally, the number of electrons surrounding the nucleus is equal to the number of protons in the nucleus. Thus, the atom has a net charge of zero.
In all elements except hydrogen, the nucleus also contains one or more neutrons. A neutron has no electrical charge, but is about as massive as a proton. The mass of an atom is determined primarily by the sum of its protons and neutrons, with electrons having only a minimal contribution.
The properties of various substances are determined by the atoms of which they are composed. Gold, for example, is very heavy and dense. This is because a single atom of gold has 79 protons in its nucleus and (typically) 118 neutrons. Conversely, helium atoms have only two protons, and typically two neutrons. Helium is therefore very light: lighter than air which is made primarily of nitrogen and oxygen. That’s why helium balloons float on air.
But the other properties are not as obvious. Why, for example, is gold a good conductor of electricity? Why does it have the yellow-ish color it does? Why is polished gold shiny? All of these properties are determined by the rules governing the way in which electrons swarm around the nucleus. And this is where the rules of quantum physics come into play.
Why Quantum?
The way in which electrons “orbit” the nucleus of an atom is similar in certain respects to the way in which planets orbit the sun. Planets are bound to the sun by the attractive force of gravity, which bends their otherwise straight-line path into an approximate circle around the sun. Likewise, the negatively-charged electrons are bound to the positively-charged protons in the nucleus, causing them to orbit.
However, there are some differences as well. Planets can orbit at essentially any distance from the sun if they have the right velocity. Give a planet just a bit more energy, and it will move into a slightly larger orbit. But electrons orbiting the nucleus of an atom can only orbit at certain specific distances – and not in between. Each distance is associated with a particular energy level – and there is a minimum energy level called the ground state. The ground state represents the closest an electron can circle the nucleus of an atom. The next level is called the first excited state. The level after that is the second excited state, and so on. Thus, the energy levels at which electrons can exist in an atom are quantized (they come in discrete quantities). And this is what puts the “quantum” in quantum physics.
The Wave Nature of Matter
But why are electron levels quantized? The answer concerns the wave nature of matter. Early in the history of physics there was considerable debate about whether light was a wave, or comprised of individual particles. We now know that light is (in a sense) both. It sometimes behaves like a wave, and other times it behaves as if it were made of particles. At first glance, this might seem contradictory, because a wave is extended in space, whereas a particle has only a single location in space and is not extended.
Consider dropping a rock into a lake. The splash will form a ripple pattern of concentric circles that expands with time. If the splash is large enough, the ripples might eventually fill the entire lake. So if we ask, “Where is the ripple?” The answer is, “Everywhere – it fills the surface of the lake.” But a single particle of infinitesimal size cannot do that. It exists at only one specific location in space at any given time.
Through a variety of experiments, physicists have discovered that light, electrons, and in fact all particles have a wave nature. Under certain circumstances, they act as if they are a wave that fills a certain volume of space. At other times, they behave as if they are particles, existing at only one specific location in space. However, quantum particles never behave as both a wave and a particle at the same time. Thus, there is no contradiction.[1]
So, when do quantum objects act like particles, and when do they act like waves? The answer is apparently that they act like particles when they are observed, and like waves when they are not observed. This seems very peculiar for multiple reasons. (1) How does the particle know it is being observed so as to change its behavior? (2) How do we know it’s a wave when we are not observing it?
As to the first question, keep in mind that we cannot observe a quantum particle without affecting it. We tend to think of observation as passive. If we want to observe something large, we just shine a light on it, and the reflected light enters our eyes and informs us what the object looks like. Shining light on a large object doesn’t affect it very much because the object is so much more massive than the particles of light that impact it. But in the quantum world, particles are so small that anything we use to observe them will have a significant effect on the particle.
The Two-Slit Experiment
To answer the second question, we know that quantum objects behave like waves when we are not observing them because of where the particles end up. This was demonstrated in the famous two-slit experiment. In this experiment, there is a light source some distance from a wall. The wall has two narrow, vertical slits in it. Light can pass through the slits. These slits are microscopic – separated by a distance comparable to the wavelength of light. Another wall exists behind the first and records where the light strikes.
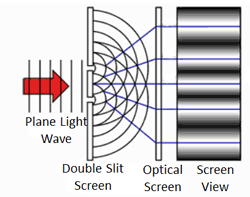
We know how waves behave in this situation from our observations of large-scale waves (such as waves in water). A wave emitted from a source will impact the wall, but sections of the wave will pass through both narrow slits – forming two new waves that move away from the slits. The two waves begin to overlap as they move toward the second wall. In some places the peak of one wave overlaps with the trough of the other, and the two opposites cancel out. In other places the peak of one wave adds to the peak of another, forming a really tall peak. Thus, there are certain places on the second wall where the waves are very strong (because the two sources reinforce each other), and other places where the waves are non-existent (because the two sources have canceled out). This is called an interference pattern. We can compute the interference pattern based on the wavelength of light.

Sure enough, the two-slit experiment confirms that light is a wave. Send light of a given wavelength toward the slits, and the wave will go through both, forming two new waves which create an interference pattern. Yet, we also know that there is a minimum energy level for light of a given wavelength. You can have one unit of energy, or two, or three, but not 1.5 or one-half, or one-quarter. This suggests that light is made of indivisible particles – each unit of energy corresponding to one particle. These particles are called photons.
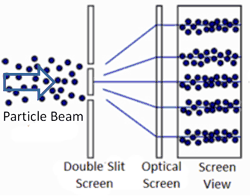
So what happens when we do the two-slit experiment, sending the light in one photon at a time? The answer is that the photon will always land on one of the places where the two waves combine constructively, and never on the places where the two waves cancel out. In other words, the photon has apparently traveled as a wave (extended in space), and has gone through both slits forming two waves that interfere with each other. Only when these waves strike the wall does the photon again act like a single particle at one location in space. And the location it picks is always where the waves are strongest. It’s amazing and counterintuitive. But this experiment has been repeated many times and this is always the result.
The equation describing the peaks and troughs of the wave is called the wavefunction. Scientists have discovered that the square of the wavefunction is exactly equal to the probability of detecting the particle at that location. So that is why the photon always ends up where the waves are strongest, and never where they cancel out.
Apparently, one photon – a single particle of light – can go through both slits because it behaves like a wave. It is extended in space and can therefore pass through both slits, forming two new waves that interfere with each other. Yet, our intuition suggests that the particle can only pass through one slit. And so it is tempting to put a detector on the slits to observe which slit the photon passed through. We actually only need a detector on one of the two slits, because if it does not detect the photon, then we know it must have gone through the other slit. So, what happens when we place a detector on one of the two slits?
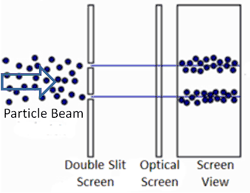
This experiment has been done. And amazingly, the photon changes its behavior. Instead of passing through both slits as a wave and then landing on one of the locations of constructive interference, the photon will pass through only one slit or the other, and will land at one of two locations on the second wall. Observing the photon at the slit causes it not to form the interference pattern!
Apparently, observing a particle “collapses the wavefunction.” It causes the object to be a particle at one location in space, thereby destroying the wave. After that observation, the particle again behaves like a wave until it is once again observed. It sounds unbelievable, but every scientific experiment ever done to test this confirms that this is indeed what happens.
Not only do photons behave this way, but apparently all quantum particles do. The two-slit experiment has also been performed with electrons. They also form an interference pattern, even when the electrons are sent through the slits one at a time. All particles have a wavefunction. The wavelength decreases with increasing energy, which is why we cannot detect the wavefunction of macroscopic objects.[2]
Waves and Atomic Structure
The wavefunction is why electrons can only orbit at certain quantized energy levels. As electrons in atoms are not normally being observed, they behave like waves. These have a specific wavelength depending on the energy of the electron. But the number of wavelengths in the circumference of an electron’s orbit must be an integer (i.e., 1, 2, 3, 4, but not 1.5). Why? Because if it were not an integer, then the peak of the wave would overlap with a trough from the previous orbit and the wave would cancel itself out. Electrons can only orbit in discrete energy levels for the same reason that photons in the two-slit experiment only land in one of the bright zones of constructive interference.
Thus, the wave nature of electrons is responsible for the size of atoms, and to a great extent, how atoms interact with other atoms. This, along with other factors to be discussed later (such as spin and the Pauli exclusion principle), is why various substances have various properties. So, when God decided that gold should be heavy and shiny, and that hydrogen should be light and flammable, He had to design particles with a wave nature and laws of physics that would give rise to all these properties. What a mind!
A Brief History of Discovery
Most students learn in grade school about atoms and that atoms are comprised of protons, neutrons, and electrons. The existence of atoms was postulated as early as 450 B.C. by the Greek philosopher Democritus. However, scientific confirmation that all matter is made of atoms came about only in the early 1800s. Electrons were discovered in 1897 by J.J. Thomson. The proton was discovered in 1917 by Ernest Rutherford who had previously (1911) discovered that all the positive charge in an atom was concentrated in a central nucleus. The elusive neutron was discovered in 1932 by Sir James Chadwick, for which he won the 1935 Nobel Prize in physics. It may surprise many people that we have only known about the structure of an atom for less than a century.
Of course, the existence of light has been known since the creation of mankind. And the wave nature of light has been known since around 1800. But the discovery that light comes in discrete energy particles – photons – came about in 1905. Albert Einstein made this discovery – the photoelectric effect – for which he received the 1922 Nobel Prize in physics. However, the term “photon” was coined 1926.
Electrons are thought to be elementary (or “fundamental”) – meaning they are not comprised of smaller particles. Likewise, photons are elementary. But protons and neutrons are composite particles. They are made of smaller particles called quarks. There are six types of quarks, but protons and neutrons are made of only the two least massive types. There are other, more exotic particles that are made of other varieties of quarks. Most of these particles are unstable – meaning they will spontaneously change into a different type of particle while releasing energy. There are certain rules that govern what kinds of particles can exist, and how (and whether) they can transform into other particles.
A Hierarchy of Particles
As such, we will find that all quantum particles fall into certain natural families. For example, the electron is a member of a class of particles called leptons. There are six leptons. Particles made of quarks are called hadrons. And while there are many types of hadrons, there are only six types of quarks.
Amazingly, the properties of quantum particles are so mathematical that physicists have been able to predict the existence and some of the properties of quantum particles before they were discovered! For example, physicists predicted long ago that there would be exactly six types of quarks, and six types of leptons. We have now experimentally discovered all of them. In fact, all elementary particles predicted by the standard model have now been discovered.
To illustrate how amazing this is, imagine a biologist carefully studying bears, dogs, zebras, whales, and so on. Having never seen or heard about an elephant, the biologist concludes that there must exist a large four-legged grey mammal with a long trunk and tusks, based on the mathematical patterns he observes in other animals. Then later, another biologist takes a trip to Africa and confirms the existence of such a creature. Of course, nothing like that has ever happened in biology. But in physics, we can actually predict the kinds of particles God created based on math!
In the next articles, we will look at the various families of particles that God created along with their properties. We will also explore how these particles transform into others and the rules behind this. When we examine how particles are classified into a nested hierarchy; we will find that there is no secular explanation. However, the natural groups of particles make perfect sense in light of the nature of God as revealed in the Bible.
[1] A contradiction is “A and not-A at the same time and in the same sense.” An electron sometimes behaves as a wave (extended in space) and other times as a particle (not extended in space), but never both at the same time.
[2] The wavelength is equal to hc/E where E is the energy of the particle, c is the round-trip speed of light, and h is Planck’s constant. Thus, lower energy particles have longer wavelengths.