We have been exploring the claims of a flat-earth advocate named Jeff. So far, his claims have not withstood mathematical scrutiny. The evidence we have explored so far has been completely consistent with a round earth, and refutes a flat earth. Here we continue to examine Jeff’s claims.
Jeff: Here’s another picture that Jeff Williams shows. He says he took it from the space station but you can still see layers of atmosphere and he must have forgotten to use his fisheye lens because he proves the earth is flat in this picture. How can this be?

Lisle: The photo was taken from the international space station, which orbits (around the spherical earth) about 250 miles above the earth’s surface. How – precisely – does Jeff think this image proves that the earth is flat? He provided no mathematical details as to how much curvature quantitatively should appear in the image. After all, the more we zoom in on a section of a sphere, the less curvature is apparent. It should be obvious that Colonel Williams was using a telephoto lens in this image due to the vertical extent of blue atmospheric scattering.
Our atmosphere preferentially scatters the higher frequencies of sunlight, which makes our sky appear blue. But since our atmosphere thins with altitude, this effect only extends about 20 miles above the surface of the earth. At higher altitudes, the sky appears black even during the day. I have noticed on commercial air flights that the sky is noticeably darker at altitude, and commercial planes typically fly at around 7 miles above sea level. Since the sky is only blue for less than about 20 miles in altitude, and since there is still some blue at the top of this image, we must conclude that we are seeing a very small section of earth. And hence, the curvature over this small patch will also be very small. How small is yet to be determined.
Jeff: He [sic] showing thousands of miles of horizon and it’s perfectly flat.
Lisle: Thousands of miles? Where is Jeff getting that number? Let’s do the math. We know from video footage of high-altitude aircraft and balloons that the (day) sky becomes essentially black at elevations higher than about 20 miles. And there is still some blue at the top of Colonel Williams’s photo, so the vertical field of view corresponds to no more than roughly 15 miles. The horizontal field of view is about twice that, so 30 miles at most (and certainly not “thousands of miles”)! How much does the earth curve over 30 miles? The circumference of the entire earth is 24,900 miles which corresponds to 360 degrees of curvature. Thus, 30 miles corresponds to 360°x30/24,900 = 0.43 degrees. That is very slight.
A curve that departs from a straight line by less than half of one degree is difficult for the human eye to detect. Nonetheless, if you put a ruler across this image just below the brightest cloud layer, and slowly move it up so that it just barely covers the left and right sides of this horizontal layer, you will see that there is indeed curvature since the middle regions of this bright layer extend just above the ruler. It’s exactly what we would expect from geometry. Furthermore, when Colonel Williams uses lower magnification, the curvature of the earth becomes very apparent.

Jeff: Again in this picture (250 miles above the earth’s surface), as in all other high altitude pictures, the horizon always rises to eye level. This wouldn’t be the case on a round earth.
Lisle: How does Jeff know where “eye level” is in this picture? Or has he simply assumed that the horizon is at eye level? If we define eye level to be perpendicular to the direction of gravity, then on a spherical earth the horizon will appear increasingly below eye level as the elevation of the observer increases. Jeff is correct that on an (essentially infinite) flat plane, the horizon will always be at eye level regardless of the height of the observer. Thus, the spherical earth model and the flat earth model make different predictions of what we should observe. And observations confirm the spherical earth model because the horizon does indeed appear below eye level for observers at high altitudes. But how much does the horizon drop with increasing distance from the earth? Again, this is a simple geometric computation:
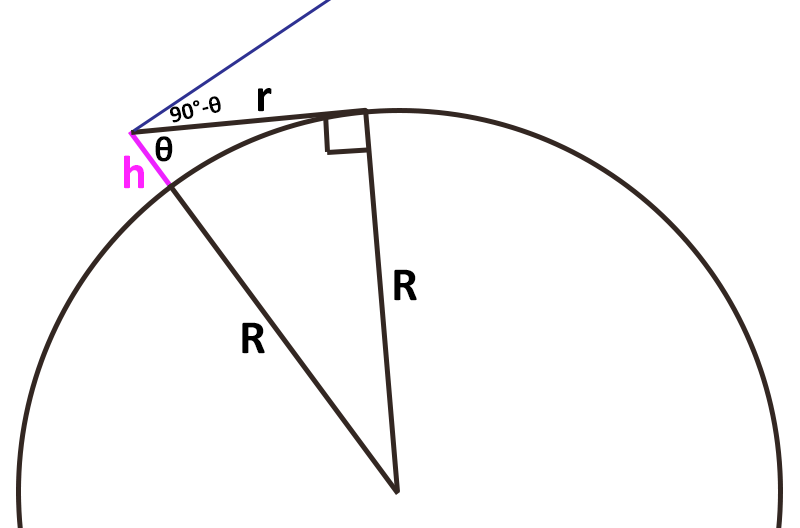
Let R be the radius of the earth (3959 miles), let h be the height of an observer above the earth’s surface, and let r be the distance to the horizon. Thus, we have a right triangle with legs R and r, and hypotenuse R+h. Let θ be the angle between segments R+h and r. From trigonometry, sin(θ) = R/(R+h). So, θ = asin(R/(R+h)) where asin refers to the inverse sine function. Since we defined eye level as being 90 degrees from the direction of gravity (along line segment R+h), the horizon will dip below eye-level by 90°-θ. This can also be expressed as acos(R/(R+h)) where acos is the inverse cosine function.
Let’s plug in some numbers. If you are standing on the ground, and your eyes are six feet above it, then the horizon dips below eye level by 0.043 degrees. That’s not noticeable. From the top of Pikes Peak, which is roughly 1.9 miles higher than the plains to the East, the eastern horizon dips below eye level by 1.77 degrees. That’s over three and a half times the diameter of the full moon. That would be easily visible if we had a frame of reference that identified “eye level” as perpendicular to gravity. And, of course, we do have such devices. You can pick up a level from any hardware store. When the bubble is in the middle, the level is horizontal. Then sight down the level. From Pikes Peak you will see that the horizon is indeed below eye-level by 1.77 degrees.[1]
A commercial aircraft has a typical elevation of about 7 miles. The horizon dips below eye level by 3.4 degrees at that height. Again, this would be easily noticeable if we had a reference for comparison. High altitude balloons can reach 20 miles in altitude, at which point the horizon drops below eye-level by 5.7 degrees. The international space station orbits at around 250 miles in elevation. At such a distance, the horizon is below eye level by a very noticeable 15.5 degrees. Thus, in wide-angle views of earth from the space station, the spherical nature of earth is very apparent.
Jeff: The word “SEX” is written upside down and it’s plain to see.
Lisle: We have already refuted that claim as it’s an example of pareidolia. Besides, those clouds are clearly a bunny.
Jeff: As far as NASA’s pictures of earth, I’ve already shown you that they change every year and the sizes of the continents change also. Clear fakery.
Lisle: This again reveals a lack of understanding of geometry, trigonometry, and perspective. And I must point out that Jeff provided no evidence, nor any computation of how large the continents should appear at a given distance from earth. Of course, the linear size of the continents doesn’t really change significantly from one year to the next. But their angular size relative to the horizon is very dependent on distance from the observer. I presume that Jeff is referring to images of earth where one of its continents appears to take up a larger fraction of the visible surface than in another image due to the fact that the two images were taken at very different distances. For example, consider the following two images:

On the left, the continent of North America appears to fill nearly an entire hemisphere of the globe. But, the image on the right shows North America filling only a small part of the globe. Is this “clear fakery?” Are these two different globes with different sized continents, or CGI images? None of the above. These are two pictures of the same globe that I took with the camera on my phone from different distances. In the left image, I am holding the camera fairly close to the globe, and am using a wide field of view. In the image on the right, I am standing much farther from the globe, but I am using a narrow field of view. Have the continents actually changed size? Of course not. They cover different fractions of the visible surface of the sphere because the fraction of the surface of a sphere that is visible depends upon distance. This is perspective.
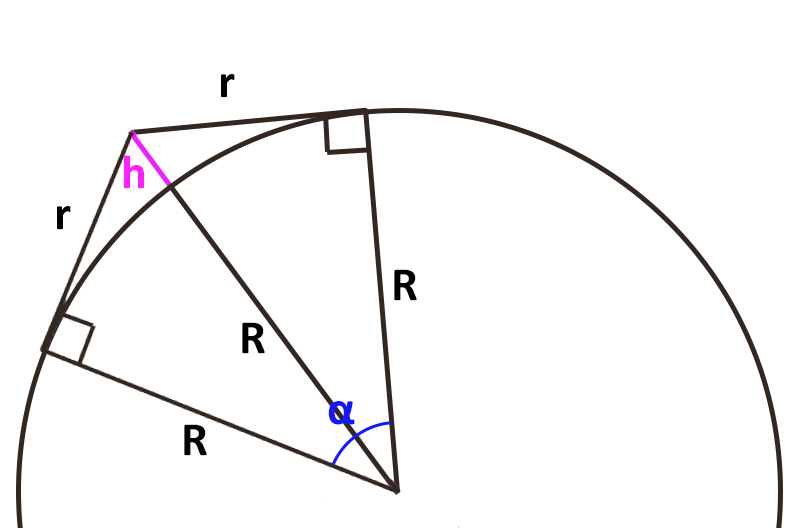
Using geometry and trigonometry, we can compute the fraction of the earth’s surface that is visible for a given distance above the ground. Let h be the height of the observer above the surface of earth, and let R be the radius of the earth. Then the angular extent of earth’s visible surface as defined from its center will be α = 2 acos(R/(R+h)). Only when this angle approaches 180 degrees do we truly see an entire hemisphere. Otherwise, we are seeing a much smaller fraction of it.
For example, the astronauts on the International Space Station are at an altitude of about 250 miles, and can therefore see 39.7 degrees of the earth’s surface at any given time. That’s only 22% of the 180-degree extent of a hemisphere, corresponding to a distance from one horizon to the other of 2740 miles. So, a continent could potentially fill the entire visible section of the earth from their perspective.
On the other hand, when the Apollo astronauts were on (or orbiting) the moon, their distance from earth was about 240,000 miles, allowing them to see 178 degrees out of 180 degrees – essentially an entire hemisphere of the earth. Thus, in photos like Earthrise, we see the continents in their true proportion to the size of earth.
Conversely, if the earth were a flat disk, then the astronauts on the space station should be able to see all the continents at all times. Yet, they can’t. Images of the earth taken from space are always consistent with a globe, and are never consistent with a flat disk.
Jeff: Your explanation of the two earth pictures doesn’t make sense to me. The one from Apollo 8 shows a very small earth from the orbit around the moon. However, in reality from the other picture taken 1 million miles away, the earth is much much [sic] image when compared to the moon. Therefore, if looking at the earth from the moon, the earth should look extremely large . . . unlike in the Apollo 8 photo.
Lisle: We answered this in the previous article, and showed mathematically that the angular size of the earth and moon are exactly what they should be. The Apollo 8 photograph was taken from a position very close to the moon, and has a field of view of nearly 16 degrees along the diagonal. The diameter of earth is nearly two degrees from that distance, which is about 1/8 the diagonal length of the image. The image from the DSCOVR spacecraft was taken from a distance of around a million miles, at which point the earth subtends an angle of only 0.5 degrees. But the DSCOVR is using a camera with much higher magnification, and a field of view of only 0.62 degrees. So, the diameter of earth is roughly 80% of the size of the frame, just as it should be.
Jeff: You didn’t comment on the fact that NASA considers the Van Allen belt to be dangerous radiation and they need to understand that first before sending humans through that region.
Lisle: Where did Jeff get that idea? The Van Allen belts do contain radiation. But for them to be dangerous to humans, we would need to know the quantitative details. Namely, (1) how much radiation is within the Van Allen belts, and (2) how much radiation is dangerous to human life? Without those numbers, we cannot rationally argue that it is dangerous for humans to travel through the Van Allen belts. So, let’s do the math.
Many unmanned spacecraft have passed through the Van Allen belts and measured the radiation levels. So, we know that the radiation within the Van Allen belts varies by location from 0.0001 Rads/s to about 0.05 Rads/s. During the Apollo missions, the astronauts spent just over one hour traveling through these belts, and the spacecraft received a total radiation exposure of about 16 Rads.[2] Moreover, the spacecraft itself offers significant insulation, so the astronauts would be exposed to much less than 16 Rads. In fact, the radiation dosimeters carried by the astronauts reported a total radiation exposure for their entire trip as only 2 Rads.[3]
How dangerous is that? A dosage of 300 rads or higher within one hour is potentially lethal. However, radiation doses below 25 rads per hour produce no noticeable effects on human physiology. So even if the astronauts had no protection from the spacecraft, they would have suffered no ill effects from traveling through the Van Allen belts. Again, when we go through the math, we see that there is no problem.
Jeff: Doesn’t that seem odd to you since we already supposedly did that with the ’69-’72 moon missions?
Lisle: No. Since the radiation in the belts is well below the limit at which physical effects are produced, there is no problem. I wouldn’t want to spend a long time in the Van Allen belts; but a brief trip through them is not a problem at all.
Jeff: NASA also admits they can’t leave low earth orbit. Again, they’ve already done that supposedly. These are things that make no sense.
Lisle: To be clear, NASA and other space agencies continue to send unmanned spacecraft far beyond low earth orbit, some leaving the hill radius of earth completely. I suspect what Jeff means is that we currently (as of 2021) do not send manned spacecraft beyond low earth orbit any more. And there is a very good reason for this. It takes a great deal of equipment to provide an environmental bubble suitable for protecting human life from the harsh vacuum of space. Equipment to supply oxygen and remove carbon dioxide, to keep the internal pressure around 1 atmosphere, to keep temperatures around 70 degrees Fahrenheit, to provide food and water, and so on are all necessary for manned flights, but not for unmanned probes. Such machinery is quite heavy, and thus it takes a great deal of energy to propel such mass into space, and far more so if such machinery is to leave low earth orbit.
Currently, the only rocket powerful enough to send people to the moon is a Saturn V rocket. These were used for the Apollo missions. But we currently have no working Saturn V rockets because they are prohibitively expensive to build and to maintain. So, this makes perfect sense.
The Apollo program cost around $28 billion, which would be roughly $280 billion today when adjusted for inflation. However, NASA’s current yearly funding is around $22.6 billion. So, NASA has less than 10% of the funding it had for the Apollo missions when adjusted for inflation. We have the technological knowledge to return to the moon; finances are the issue. And there are plans to return men to the moon with the upcoming Artemis program.
There are many observations you can make and experiments you can do to test the shape of the earth. I mentioned many of these in a previous article, and at least one additional test here. Try them! Many aspects of science are difficult to test without expensive equipment. But the shape of the earth is not one of them. Don’t just accept unsubstantiated claims from non-peer reviewed websites when you have the capacity to test such claims. More to come.
[1] Since I live in Colorado Springs, I had intended to perform this experiment and post the pictures here. But poor weather and smoke from wildfires prevented a clear view. I would encourage anyone living near a tall mountain to perform this simple experiment on a clear day, and see the curvature of the earth with your own eyes.
[2] https://www.nasa.gov/sites/default/files/files/SMIII_Problem7.pdf
[3] Ibid.

