In this article, we will deal with the claims of a flat-earth advocate named Jeff. Jeff is a friend of a friend of mine, who objected to some of the proofs I gave that demonstrate the earth is spherical. Since Jeff’s claims have been refuted elsewhere, I agreed to answer them but only if I could post them publicly on this website so that others may benefit. Jeff graciously agreed.
Jeff: One of things I refute is when he [Lisle] says when a boat comes into view, you see the mast first and then eventually the entire boat. This has been proven to be just the law of perspective and not due to curvature.
Lisle: Perspective refers to the angular size of an object as a function of its distance. It is not magic and will not explain why the mast of a boat is visible even when the rest of the boat is obscured by the ocean. Rather, perspective explains why the boat appears smaller at greater distances. This is because it subtends a smaller angle with increasing distance. If one object is twice as far as another identical object, it will appear half as tall and half as wide as the closer one. But the size will never go to zero for any finite distance, and the object could never be obscured by a flat horizon. Perspective is an aspect of geometry and is computed using trigonometry.
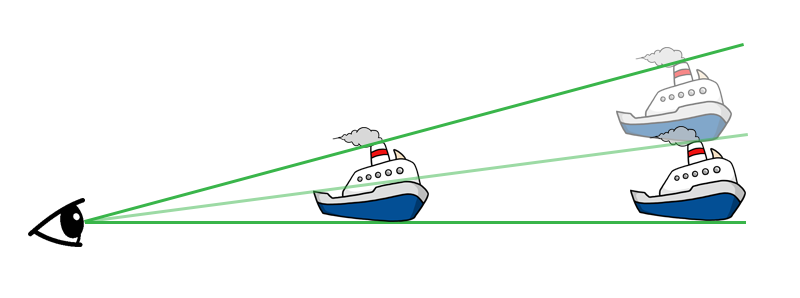
Due to perspective, objects at a given height above the ground will subtend a larger angle with the horizon when closer to an observer than they do when farther from that observer.[1] For example, a cloud that passes overhead appears ninety degrees away from the horizon. But as it moves away, it appears “closer” to the horizon even if its distance from the ground remains constant because it subtends a smaller angle. But it can never appear to touch or be obscured by a flat, infinite horizon.
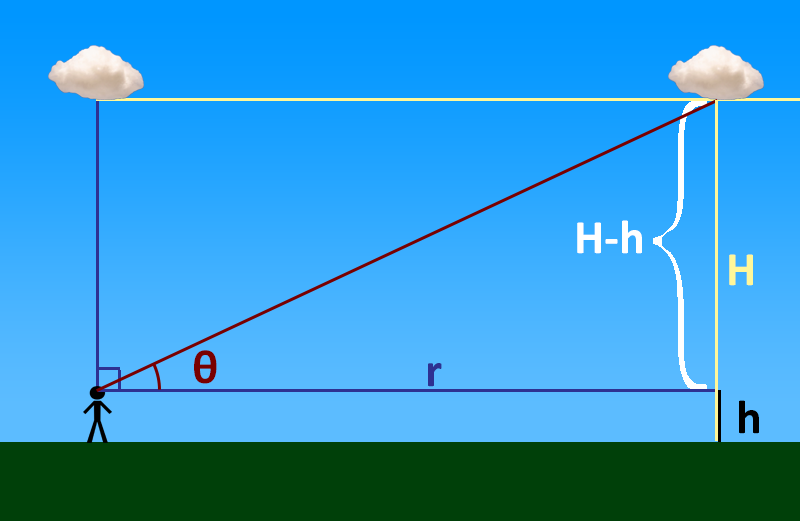
On a flat plane, the angle between the horizon and an object at height H and distance along the ground r as seen by an observer at height h is given by the formula: θ = atan((H-h)/r) as illustrated in the figure. Here atan is the inverse-tangent function or “arc-tangent.” So, for a cloud that is one mile above the ground, and three miles distant, that cloud will appear 18 degrees above the horizon. A cloud that is fifty miles distant would appear 1.1 degrees above the horizon on a flat earth – about twice the diameter of the full moon. You can do these computations also for the mast of a ship if you know its height above water level. But the angle will never go to zero on a flat earth. Thus, the mast of a ship could never be obscured by the ocean on a flat earth because it will always be above the horizon.
What about the base of a ship – where it contacts the water? This has a height of zero. So an observer at ground level should always see the base of a ship on a flat ocean. It could never go below the horizon because the inverse-tangent of zero is zero. Thus, Jeff’s claim about the mast of a ship being visible at greater distances than the base being due to perspective is false. On a flat earth, the base and mast of a ship would be equally visible at all distances from any observer.


Perspective explains why ships look smaller when they are farther away. It does not explain why they dip below the ocean horizon at some distance. Only a round earth can account for that.
Jeff: Put a telescope on the boat and it’s [sic] entirety will be seen. Same way when a boat is sailing away, the bottom always disappears first to the naked eye. However, put and telescope on it, and it comes back into view in it’s [sic] entirety. Hence, this is a false claim by Jason.
Lisle: I notice Jeff produced no evidence to back up his claim. Take a look at Dr. Faulkner’s pictures taken through his telescope of a ship traveling away. You can clearly see the departing ship go over the horizon, with the bottom part obscured first until only the mast is visible. Thus, Jeff’s claim is false.

Dr. Faulkner’s article is available here:
https://answersingenesis.org/blogs/danny-faulkner/2021/06/10/more-evidence-earth-is-a-globe/
Jeff: We can see way too far for the earth to be the round size science claims.
Lisle: Evidence? Exactly how far does Jeff think we should be able to see, and what calculation has he done to establish this? Or is it just an emotional feeling? In any case, if the earth were flat, we should be able to see all its features from any distance with a sufficiently powerful telescope since they all would be above the horizon. Why can’t we?
When I was in Memphis, TN a few weeks ago, why couldn’t I see Pikes Peak? The distance between the two locations is about 867 miles, and Pikes Peak is 2.62 miles higher in elevation than Memphis. Computing the perspective, we find that Pikes Peak should appear 0.17 degrees above the horizon from Memphis on a flat earth. That would be easily visible to the unaided eye.[2] Yet it wasn’t.
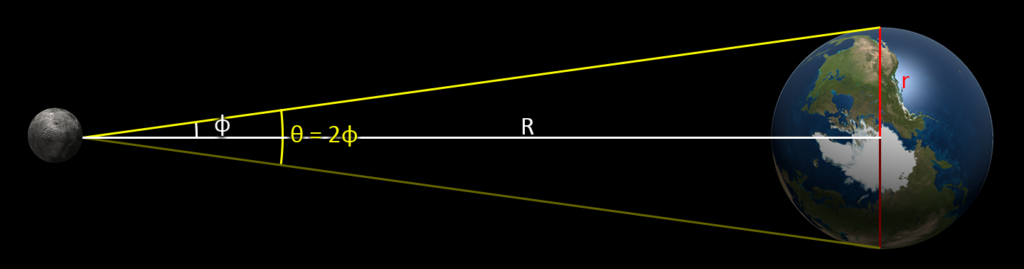
How far can we see on a round earth? First, let’s consider viewing a spot on the ground (elevation = 0) from some distance away. We will want to do this somewhere without hills and valleys (as flat as possible so that only the curvature of the earth matters); somewhere like western Kansas would work, or the ocean on a calm day would be ideal. Furthermore, we will pick a day when the ocean/ground temperature is about the same as the air temperature, so that the light is not significantly refracted but travels in straight lines.[3]
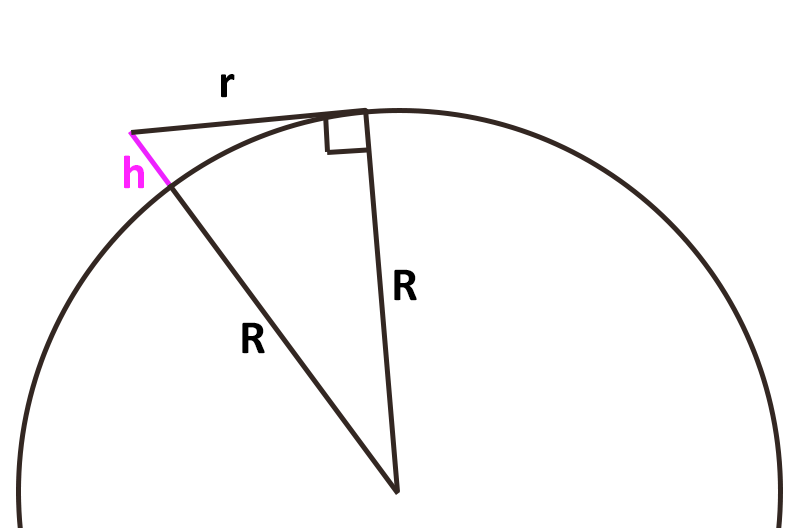
In the above illustration, h is the height of the eyes of the observer above the surface of the earth, R is the radius of the earth, and r is the maximum distance a spot on the ground can be seen. From the Pythagorean theorem we have r2+R2=(h+R)2. Solving for r, we have r = √(h2 + 2hR). So, if your eyes are six feet above the ground (0.00114 miles), and the radius of the earth is 3959 miles, then you can see a spot on the ground up to three miles away. Beyond that, the spot is over the horizon, obscured by the curvature of the earth. Remember that this computation assumes absolutely no relief (no hills or valleys) in the terrain and matching ground and air temperatures.
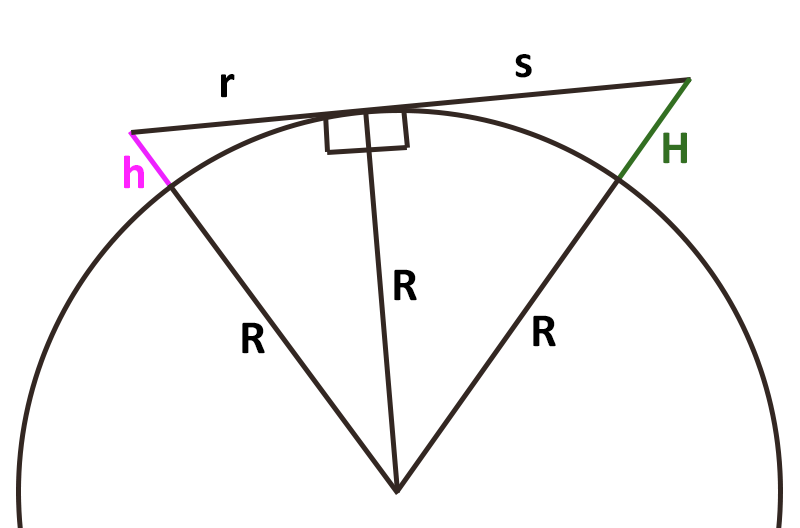
From geometry, if an object has some height above the ground, it can be seen from a greater distance than a spot on the ground as illustrated in the above figure. Let’s call this extra distance s, and the height of the object H. So the total distance to the object will be r+s. Again, from the Pythagorean theorem we have s2 + R2 = (H+R)2. Solving for s we have: s = √(H2 + 2HR). So, standing on a raft in the ocean with your eyes six feet above sea level, you could see the eyes of your twin up to six miles away (but no farther) on a day with no waves and no temperature gradients.
Using this formula, what is the maximum distance a mountain as tall as Pikes Peak could be seen from Memphis? R = 3959 miles, r = ~3 miles, H = 2.62 miles, so: r+s = 147 miles. Since Memphis is actually 867 miles from Pikes Peak, one cannot be seen from the other. The curvature of the earth is why you cannot see Pikes Peak from the plains at distances greater than about 150 miles, with the exact number depending on elevation. Thus, you cannot see Pikes Peak from Dodge City, Kansas, because it is 283 miles away. On the other hand, if the earth were flat, Pikes Peak (2.12 miles higher than Dodge) should be 0.43 degrees above the horizon. That’s just slightly less than the diameter of the full moon, which would be easily visible to the unaided eye.
So if you want to test the curvature of the earth for yourself, go to Dodge and look west. If you see Pikes Peak looming above the horizon and nearly as large as the full moon, then the earth is flat. But if the earth is round, Pikes Peak will not be visible.
Jeff: You mention we have pictures of the earth. How about this one? It’s an official NASA photo with “SEX” written in the clouds. Show this to Jason. How do you explain this?

Lisle: First, I must point out that the earth is round in this image. As to the perception of words in the cloud formations, this is an example of pareidolia. The human mind is very good at detecting patterns, particularly those with which we are familiar, like faces or letters. This is why we can solve “captchas” whereas computers have difficulty doing so. But the drawback of this gift is that we can also perceive patterns where there are none. The ever-changing complex shapes of clouds are particularly susceptible to this phenomenon. Many children have watched the clouds change shape and imagined they are seeing a rabbit or a dragon, etc. It’s great fun. But the shapes we see in random cloud formations are far more indicative of ourselves than of the actual clouds – much like a Rorschach ink blot test. Someone even posted a photo from a plane of a cloud formation resembling an Imperial AT-AT attacking the rebel base on Hoth. But if the photographer had never seen the Empire Strikes Back, it is unlikely he would have perceived this.

I would never have seen a word in the clouds of the picture Jeff shared if it had not been pointed out to me. There is a section that sort of resembles letters, but only vaguely. To me they look more like a right-side up “X” with a subscript 35. But of course, as an astrophysicist I work with variables that often have subscripts. Our perceptions are influenced by our experiences. Given enough pictures of clouds, you will inevitably see something that vaguely resembles something with which you have familiarity. There is no conspiracy here, only psychology.
Jeff: Mathematically, it would be nearly impossible to see one letter but this one has 3 letters and it even spells a word.
Lisle: On the contrary, given the phenomenon of pareidolia, and the wide variety of random shapes found in nature, it is mathematically inevitable to find shapes resembling letters and even short words if you examine enough cases. For example, did you know that photographers, such as Kjell Bloch Sandved, have found every letter of the English alphabet and the ten Arabic numerals in butterfly wings?[4]

Is this some grand conspiracy? Of course not. It is mathematically inevitable when you consider how many butterfly wings were examined. Once you have letters, it is relatively straightforward to get a few very simple words, as anyone who has played Boggle knows. The longer the word, the lower the probability, and so complex sentences are ruled out. But short words are easy to find. Here is an example of a cat with a natural label in its fur.

Here is an example of a turtle with its Creator’s name in its shell pattern, followed by a cat’s meow.

It is mathematically inevitable to find patterns that resemble letters or short words if you examine enough random samples. That is the nature of randomness when combined with human psychology.
Jeff: How about these 2 official NASA photos of earth?
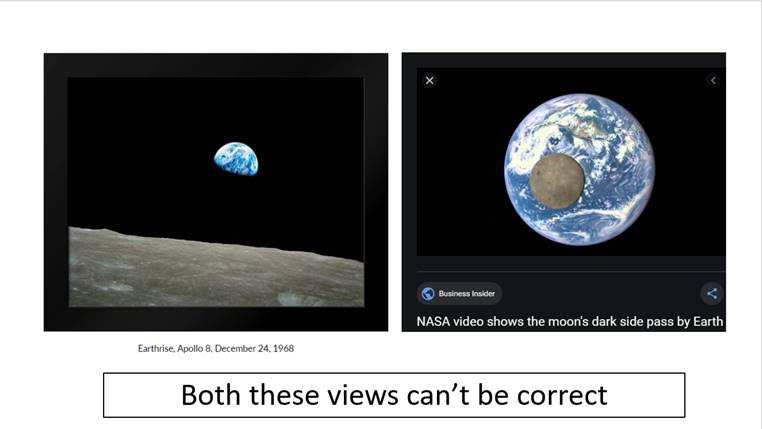
You actually showed the one on the left in your interview with Jason. Look how small the earth is in the “official” photo taken from the moon you showed. The “official” photo on the right shows a much truer size perspective of the earth to the moon from 1 million miles away. The pictures contradict each other.
Lisle: Again, this is a failure to properly understand perspective. For example, do the following two pictures contradict each other?

And yet, I took both pictures with the camera on my smart phone. So, of course they are both correct. A smaller object can appear larger in angle than a larger object if the camera is very close to the smaller object and much farther from the larger one. That is perspective.
Jeff: From the moon, the earth would have to look massive, not at all like the picture on the left.
Lisle: Exactly how “massive” should the earth look from the moon? Jeff gave no numbers, nor any evidence that he has computed how large the earth should appear from the moon. But it’s not hard to compute this. The earth and moon are separated by an average distance of R=238,900 miles. And the earth is r=3,959 miles in radius. Thus, the angular size of the earth as seen from the moon will be 2 atan(r/R), which is 1.9 degrees. So the earth would appear nearly two degrees in diameter as seen from the moon, which is about twice the width of your pinky finger held at arm’s length. That’s really not very “massive.”
Is that angular size consistent with the famous Earthrise photo? The camera used 70 mm film and a 250mm lens, which gives a field of view of 2 atan(70/250×2) = 15.94 degrees. This is the angular distance across the diagonal of the image. Thus, in the full, uncropped photograph (https://www.nasa.gov/images/content/297755main_GPN-2001-000009_full.jpg), the width of earth should be about 1/8 the diagonal length of the frame. And that is precisely what we find. You can measure it yourself with a ruler. So, contrary to Jeff’s assertion, the earth is precisely the size it should be in the Apollo 8 Earthrise image.
The right-hand image of the earth and moon in the photo Jeff shared was taken on July 16, 2015 by the DSCOVR spacecraft’s Earth Polychromatic Imaging Camera (EPIC) from a distance of one million miles.[5] The camera has a field of view of 0.62 degrees.[6] At a distance of roughly 1 million miles, the angular diameter of the earth is 2 atan(3959/1,000,000) = 0.5 degrees. The distance of the spacecraft changes a bit, so the angular size of the earth varies from 0.45 degrees to 0.53 degrees.[7] Thus, the earth should appear a bit smaller than the frame of the image, which is exactly as it appears.
Furthermore, since the moon orbits earth at a distance of nearly a quarter of a million miles, its distance to DSCOVR must be roughly 750,000 miles in this image. The moon’s radius is 1079 miles, and so it should subtend an angle of approximately 2 atan(1079/750,000) = 0.16 degrees, or roughly one third the diameter of the earth. This is exactly what we see in the image.
In reality, the moon is roughly ¼ the diameter of the earth, not 1/3. But it appears 1/3 the angular size in this image because the moon is 240,000 miles closer to the spacecraft than earth is. This is the correct application of perspective. So, when we actually go through the math, we find that the images are exactly as they should be.
Many students complain in their algebra and geometry classes, “When am I ever going to use this stuff? Why do I need to know this?” This is why! These flat earth claims are easily refuted with just a very basic high-school-level knowledge of geometry and trigonometry. The fact that so many people have been fooled by internet flat-earth claims is an indictment on our education system. You will never meet a flat-earth advocate who understands geometry and trigonometry.
[1] This is true as long as the height of the object is different from the height of the observer.
[2] A healthy human eye can detect angles roughly 20 times smaller than this.
[3] This is very important. Temperature inversions will cause light to bend in the same direction the earth curves, resulting in greater observable distances. These can be computed from physics principles, but the math becomes more complicated. So it is best to pick a day when the temperature is very stable.
[4] https://mymodernmet.com/kjell-bloch-sandved-butterfly-alphabet/
[5] https://www.nasa.gov/feature/goddard/from-a-million-miles-away-nasa-camera-shows-moon-crossing-face-of-earth

