In 1957, the Soviet Union launched Sputnik, the first manmade object to achieve earth orbit. People all over the world could see this satellite as it passed overhead. Sputnik was equipped with radio antennas to broadcast a series of pulses which could be detected by amateur radios. In the years that followed, many other spacecraft – some manned, some unmanned – were placed in earth orbit. Many of these took photographs of the earth. For the first time, human beings were able to see pictures of the earth from above. These pictures confirmed what the Bible had taught millennia earlier; the earth is round and hangs upon nothing (Job 26:7,10).
Today we have hundreds of satellites orbiting the earth. On a clear summer night, you can even see many of them as a faint star slowly drifting across the sky. Most cell phones can now determine your exact location on earth by accessing a Global Positioning System (GPS) of satellites. And yet, for all these technological advances, there are some people who claim that the earth is a flat disk. Where does this belief come from, and how are we to respond?
Internet “Education”
The internet is a wonderful tool. It allows nearly instantaneous access of information that would have taken a great deal of time and effort to research in the past. The internet allows immediate access to scholarly articles, research papers, scientific discoveries, and so on. But there is a downside. The internet also allows people to promote and easily distribute claims that are demonstrably false. Anyone can post anything on the internet. There is absolutely no requirement that claims need to be accurate and error-free. And this distinguishes the internet from many other types of documentation.
To publish a paper in a scholarly journal, the paper must pass a process of peer-review. Experts in the relevant field vet the paper to make certain it is logical, that its arguments are well-supported by evidence, and that it is coherent. A paper that fails those criteria is rejected and not published. In the past, even publishing a book took some effort. A writer would have to contact a publisher and convince him or her that the book is worth publishing. A reputable publisher wants the publications to be accurate, and therefore would take some effort to investigate the claims in question. Although these procedures do not guarantee accuracy, they do tend to drastically reduce the most absurd and indefensible claims from seeing the light of publication. This is why you will not likely see a scholarly paper defending a flat earth in a science journal, and there are very few books that would defend such a position. Let’s be honest. If you heard or read an argument for a flat earth, it most likely came from the internet. While there is nothing wrong with reading internet articles, we need to be far more discerning. Be sure to check such claims with information from peer-reviewed literature.
What does the Bible Teach?
One of the strangest claims that you will find on some internet posts is the claim that the Bible supposedly teaches a flat earth. This is odd indeed because the Bible clearly indicates that the earth is round. Job 26:10 poetically describes God inscribing a circle on the face of the waters at the boundary between light and darkness. This boundary is what scientists today call the “terminator.” It is the location on the earth’s surface where evening and morning occur, shown by the red dashes in figure 1. In other words, a person standing on the terminator is either experiencing a sunrise, or a sunset. The shape of the terminator is a circle, just as the Bible states in Job 26:10. And it occurs primarily on the waters of the earth because the earth’s surface is 71% water. A sphere is the only shape where the terminator will always be a circle.
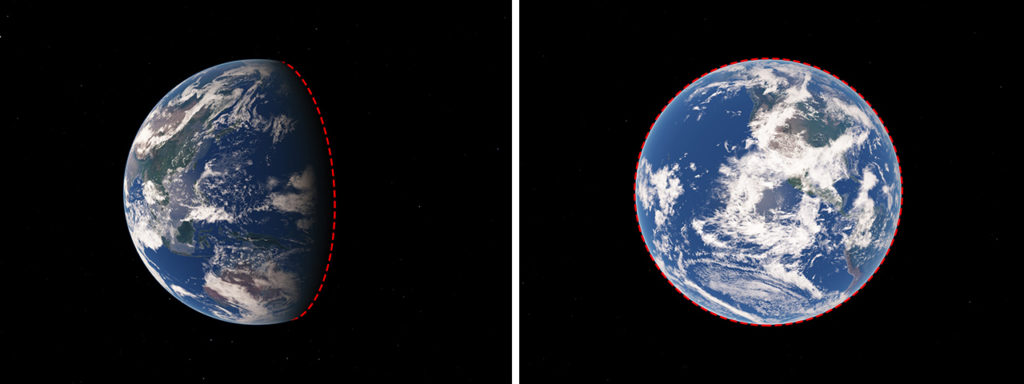
The roundness of the earth is implied in other passages as well. Genesis 6-8 describes a global flood in which all the high hills under the entire heaven were covered (Genesis 7:19). Of course, you cannot have a global flood without a globe. If the earth were flat, the water would run off the sides unless there were a rim around the edge – which would constitute a hill that is not covered with water, contrary to Genesis 7:19.
How then could anyone claim that the Bible teaches a flat earth? Some internet articles list many verses that supposedly teach a flat earth, but when you look up the verse you will find nothing of the sort. Here are a few examples:[1]
“Earth Created Before the Sun: Genesis 1:1-19.”
Uhm. Yes, the earth was created before the sun. But how does that even remotely imply that it is flat?
“Universe is Complete, Not ever expanding: Genesis 2:1”
Well, “complete” doesn’t mean “not expanding”, but even so, how does this even remotely imply that it is flat?
“Earth Measurements Unknown: Job 38:4-5, 38:18, Jeremiah 31:37, Proverbs 25:3”
Actually, the Job passages do not teach that the earth’s measurements are unknown (though they were probably unknown to Job at that time). Rather, God is asking Job where he was when God measured the earth. But none of these verses even remotely imply a flat earth.
“Extremely Large Area of Land is FLAT, no curvature: Ezekiel 45:1”
When you read the verse does it say that such land is flat or that it has no curvature? Not at all.
“Sun moves backwards: 2 Kings 20:8-11”
How is this even remotely related to the shape of the earth?
The overwhelming majority of the verses cited are like this. They say absolutely nothing about the shape of the earth. Perhaps the person who listed these thought that we wouldn’t check. Perhaps the person is so inundated with his own viewpoint that he or she reads it into every verse. But clearly, none of these verses even remotely imply a flat earth. But there are a few that someone might think actually say something about the earth’s shape… until we read them in context. For example:
“Earth has a Face (a geometrical flat surface): Genesis 1:29”
This sounds good, until you realize that the person making the claim has absolutely no exegetical support for his claim that a “face” is a “geometrically flat surface.” On the contrary, the Hebrew word translated “face” or “surface” in Genesis 1:29 is “panim” and literally means “face” or “surface” without any requirement of flatness. In fact, the same word is used of the human face in passages like Genesis 9:23, 17:3, 32:20, 33:10, 38:15, 43:31, 44:23, 46:30, 48:11, 50:1. Is the human face flat or curved? Yes, it is curved. And so this argument backfires on the flat-earther.
“High Altitude Perspectives: Daniel 4:11, Daniel 4:20, Matthew 4:8”
The passage in Daniel 4:11 describes a tree that grew so large that it was visible to the whole earth. If the tree had height, but no substantial width then indeed it could not be seen by people on the other side of the sphere. By the way, where is this tree and why can I not see it? Well, when we read the verse in context, we find this is not God describing the actual earth. Rather, it is Nebuchadnezzar giving a description of his dream. Perhaps Nebuchadnezzar did dream of a flat earth, but how does that have any bearing on the actual shape of the earth? Furthermore, Daniel explains in verses 20-22 that this tree is not literal, but symbolized King Nebuchadnezzar. How could the flat-earther have missed this?
In Matthew 4:8 Satan tempts Christ by taking Him to a high mountain and showing Him all the kingdoms of the world and their glory. Presumably the flat-earther thinks that it was the height of the mountain that made it possible for Christ to see all the kingdoms of the earth, which would only make sense on a flat earth. But does the text actually say that this is the reason? If so, then where is this mountain? If there were a mountain from which you could see everywhere on earth, then wouldn’t everyone on earth be able to see the mountain? So why can’t we? The parallel account in Luke 4:5 states that Satan “showed Him all the kingdoms of the world in a moment of time” suggesting that this was a vision, not a location from which all kingdoms can be seen physically.
Such horrible misrepresentations of Scripture may stem from the fact that the modern flat earth movement was largely developed by non-Christians in an attempt to discredit the Bible. Eric Dubay is the founder of the modern flat earth movement, and he denies that Jesus ever lived. Apparently, some Christians heard some of these bad arguments supposedly based on Scripture and thought that they were legitimate. They are not.
The History of the Science
So when and how did scientists discover that the world was round? Many people are under the impression that Christopher Columbus intended to prove that the earth is round – that this was the purpose of his voyage. This is false. Educated people already knew that the world was round by the time of Columbus.[2] People have known this from very ancient times. So when was this discovered and how? Can we really prove that the earth is round today?
As far as I know, the earliest reference to a round earth is the book of Job, especially Job 26:10 which describes the circular terminator as discussed above. Job was written in approximately 2000 B.C. Other early civilizations such as the Babylonians and early Greeks taught that the earth was flat. For example, the Greek scholar Anaximander (610 – ~546 B.C.) taught that the earth was flat. Specifically, he claimed the earth to be a cylinder with mankind living on one of the (flat) ends. It is very ironic that some flat-earthers claim that the round earth is a pagan idea, when in reality the pagan cultures clearly taught a flat earth while the book of Job describes the round earth.
It was not until the time of Pythagoras (~570 – ~495 B.C.) that the Greeks came to accept what the Bible had taught for the previous 1500 years. The earth really is spherical. It seems that the followers of Pythagoras accepted a round world, though their reasons for believing this are not recorded. The first recorded scientific arguments for a round earth come from Aristotle (384 – 322 B.C.). He noted that the positions of the constellations appear to shift as a person travels south in a way that is consistent with the surface of earth being a sphere. He also noted that the shadow of the earth on the moon during a lunar eclipse is always a circle; this won’t work on a flat earth and is proof positive that the earth is spherical as we will show below.
By the time of Eratosthenes (276 – 194 B.C.), the Greeks were well aware of the spherical nature of the earth. Eratosthenes then used observed measurements of the height of the sun as observed in Syene and Alexandria respectively on the same day to compute the size of the earth. Since these two cities are at two different latitudes, the angle of the sun at noon is different due to the curvature of the earth. By measuring the difference in angle, and knowing the distance between the two cities, Eratosthenes accurately computed the size of the entire globe. We can use a variation of his method to demonstrate that the earth is indeed round, as we will show below.
Maps of a Round Earth
There are many ways to conclusively prove that the earth is round. But first, we need some background information on terms and types of maps. The position of anything upon a globe can be specified using two coordinates: latitude and longitude. The latitude is the (smallest) angle that an object makes between the center of the earth and the equator. So if you are standing on the equator, your latitude is zero. At the north pole, your latitude is 90 degrees. Latitudes south of the equator are negative, and the latitude of the south pole is -90 degrees. To travel one degree in latitude, you must travel 68.7 miles north or south. You can confirm this yourself by driving 68.7 miles directly north or south, and noting the one-degree change in latitude.
Longitude is the angle along the equator compared to Greenwich, England. Longitudes west of England (such as the United States) are negative, and those longitudes east of England are positive, up to 180 degrees. At the equator, one degree of longitude is equal to 69.2 miles. But at other latitudes, the distance is less due to the curvature of the earth. Specifically, a difference of one degree in longitude corresponds to a distance that is the 69.2 miles multiplied by the cosine of your latitude. This is itself proof that the world is round because on a flat earth the distance corresponding to a difference of one degree in longitude would be different; it would be larger than 69.2 miles for latitudes south of the equator, whereas on a round earth it is smaller.
It is possible to map the positions of earth’s landmasses onto a flat surface; this is called projection. But since the earth’s surface is spherical, projection onto a flat surface always involves distortion in either the shapes or sizes (or both) of earth’s features. A common projection is a simple equidistant cylindrical projection, also called an equirectangular projection, in which longitudes mark the x-coordinate and equally-spaced latitudes mark the y coordinate. This results in a rectangular map with features near the equator looking accurate as shown in the figure. However, features near the poles become stretched horizontally, making them look much wider than they really are, as shown in the top panel of figure 2. This is because the actual distance between longitudes decreases near the poles due to the earth’s curvature. This projection is one of the more commonly used in world maps.
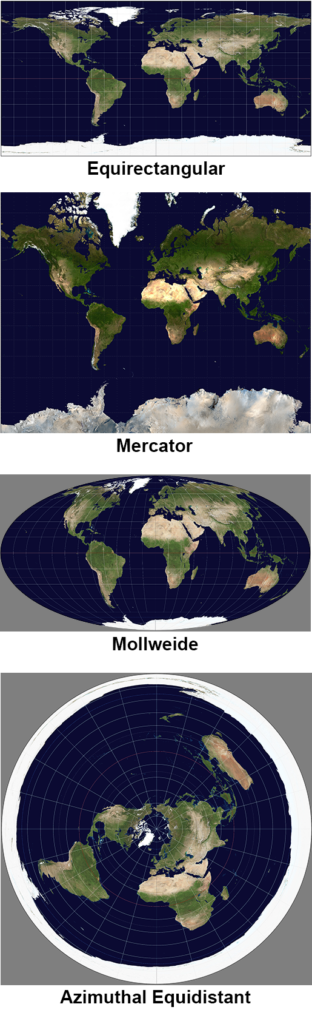
A similar method is called a Mercator projection (see figure 2, panel 2). It too represents longitudes as the x-coordinate, but latitudes are plotted unevenly, with greater spacing near the poles, such that they match the horizontal stretching with latitude. This causes small features to approximately maintain their shape at any latitude, but it results in even greater distortion in overall size.
The Mollweide projection is also very common, particularly in astronomy. Rather than projecting the globe onto a rectangle, the globe is projected onto an ellipse, as shown in the third panel of figure 2. The meridians are also ellipses. This has the advantage that it preserves area; there is no enlargement or reduction of any feature with latitude. So, this allows for fair comparison of sizes of land masses regardless of their location. The disadvantage is that it severely distorts the shape of the landmasses, particularly near the perimeter of the map.[3]
The azimuthal equidistant projection is a polar coordinate system usually centered on earth’s north pole. The map appears circular with the north pole at center – see the bottom panel in figure 2. Circles surrounding the center represent latitudes and are equally spaced. The spokes extending away from center represent longitudes. This projection drastically distorts sizes, shrinking features near the north pole and expanding features near the south pole. Note that the south pole is the entire circumference of the map, and hence Antarctica is dramatically enlarged, forming a ring around the oceans. This map is significant because most modern flat-earthers believe that this is the true shape of the earth.
Modern Flat Earth Models
The most common view among modern flat earth advocates is that the earth is a flat disk with the north pole at the center and Antarctica forming a ring around the perimeter. This is what we see in maps using the azimuthal equidistant projection; but flat-earthers believe that this isn’t just a projection but is actually the shape of the earth. They believe that the sun is always about 3000 miles above this disk and circles from east to west around a point directly above the North Pole. If this were true, then the sun should always be visible from everywhere on earth, and there would be no night. So, to get around this fact, the flat-earthers suppose that the sun is not a sphere, but more like a “spot-light” which illuminates only those sections of the earth within its cone of light as shown in figure 3. Hence, places on the earth that are experiencing night are simply outside of the sun’s light cone. The moon also circles around a point directly above the North Pole, and behaves similar to the sun.
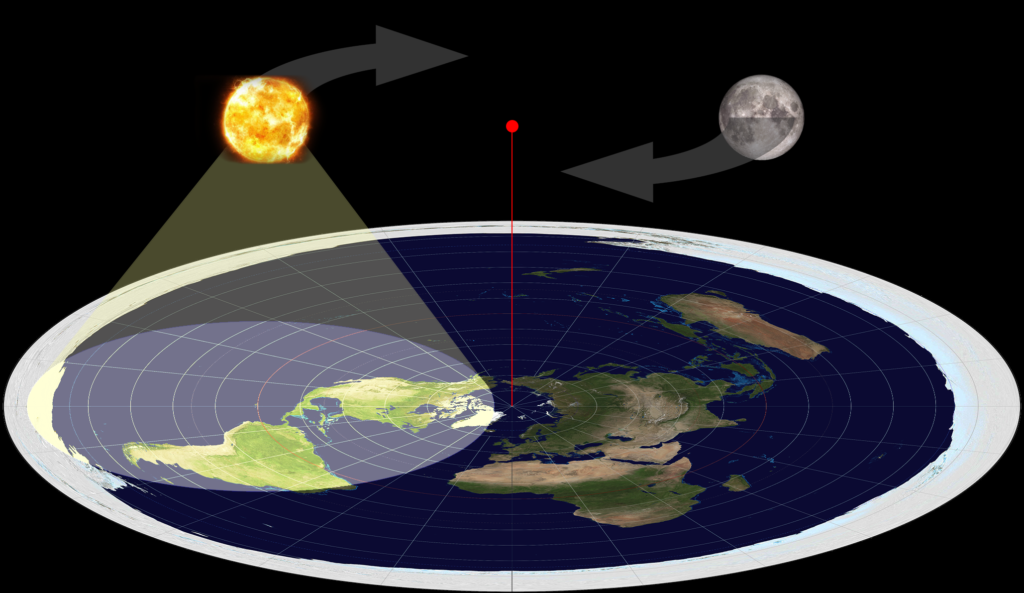
It’s a clever idea and explains why some people can be experiencing daylight while others experience darkness even if the earth were flat. But when we consider the geometrical implications of this view, we find that it is inconsistent with observations. Mathematically, the sun’s light cone would have to cover 1/4 the area of the disk in order to be compatible with the seasons (the sun is not visible from the North Pole between the autumnal and vernal equinox). This means that the average location on earth should receive an annual average of six hours of sunlight per day. On a round earth, any given spot receives an annual average of twelve hours of sunlight per day because half the sphere is illuminated by the sun at any given time. You can do some observations yourself throughout the year to see which model is correct.
One of the most obvious implications of this flat disk model is that no one could ever see a sunrise or sunset. After all, if the sun is always above the surface of a flat earth, then it can never reach or pass below the horizon. Flat-earthers claim that the sun only appears to rise or set due to perspective. But is such a claim defensible when we run the numbers?
Perspective is the phenomenon of objects subtending a smaller angle with increasing distance. An object at a fixed distance above the earth will appear increasingly lower in the sky as its horizonal distance from the observer increases. But we can calculate what that angle is. And we will find that sunrises and sunsets are not possible in the modern flat earth model. Let’s explore the details.
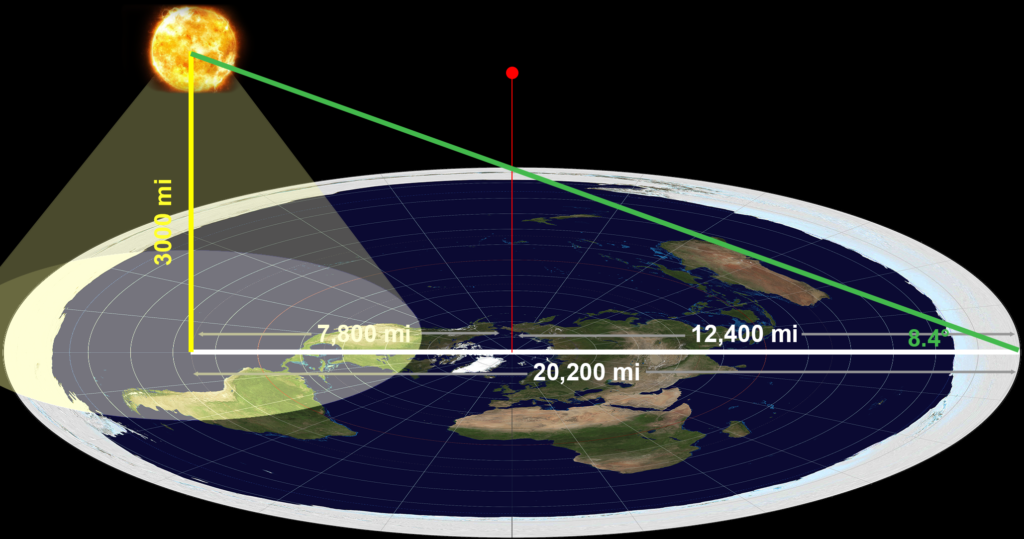
Observations have shown that the sun can appear directly overhead only from those places on earth called the tropics, which are within 23.5 degrees of the equator. Hence, in the flat earth model, the farthest away the sun can be from its orbital center above the North Pole is when it reaches the winter solstice on December 21, when it is directly above the Tropic of Capricorn. At that time, the sun will be 113.5 degrees from the North Pole, which is 7800 miles (see figure 4).[4] The farthest a person can be from the North Pole is to be on the South Pole, 12,400 miles away, as shown on the far right in the figure. Hence, the farthest a person can be from the place where the sun is directly overhead on a flat earth is 20,200 miles. If the sun is 3000 miles above the surface (yellow line) and 20,200 miles along the (flat) surface (white line), then the angle it makes above the horizon is the inverse tangent of (3000/20,200) which is 8.4 degrees. This is the minimum angle possible since it is the farthest an observer can be from the sun.
So, on a flat earth, the sun can never appear to be below 8.4 degrees above the horizon, which is about 17 sun diameters. The sunset shown in figure 5 is over the ocean, and the sun seems pretty high. But when we measure its angular altitude (bottom panel), we find it is less than eight sun diameters above the horizon. That is far less than the minimum height of 17 sun diameters for a flat earth.

Since the sun can never be closer than 8.4 degrees (or 17 diameters) from the horizon, we know mathematically that the sun cannot appear to set or rise on a flat earth. And that 8.4 degrees would be from the south pole. If we use the continental United States instead, then the farthest we can be from the spot where the sun is directly overhead is 12,300 miles and would occur at midnight. The sun would be 13.7 degrees above the horizon. So on a flat earth from the continental United States, you can never see the sun closer to the horizon than 13.7 degrees, which is 27 sun diameters. Sunrise and sunset are not possible within the modern flat earth model.
Scientific Proof of the Earth’s Shape
Although we have many pictures of the earth from space showing that it is a sphere, modern flat-earthers tend to be conspiracy theorists. They claim that all those pictures are fake, having been photoshopped. Granted, many of these pictures were available in the 1960s, decades before Photoshop had been invented, but that doesn’t seem to faze a conspiracy theorist. In fact, there are many ways that you can prove that the earth is round, and many different types of experiments that you can do to confirm this. You just need to make some measurements, and do some geometry.
One experiment you can do is a variation on the method of Eratosthenes. First, you need to know your latitude. You can look this up on a map, look it up online, or use a smart-phone app. For the sake of this example, let’s use Colorado Springs which has a latitude of 38.8 degrees. Then you need to know where the north star is. You can use a constellation map, a smart-phone app, or you can use the Big Dipper. The two stars on the end of the bowl (opposite the handle) point directly toward the North Star – see figure 6.
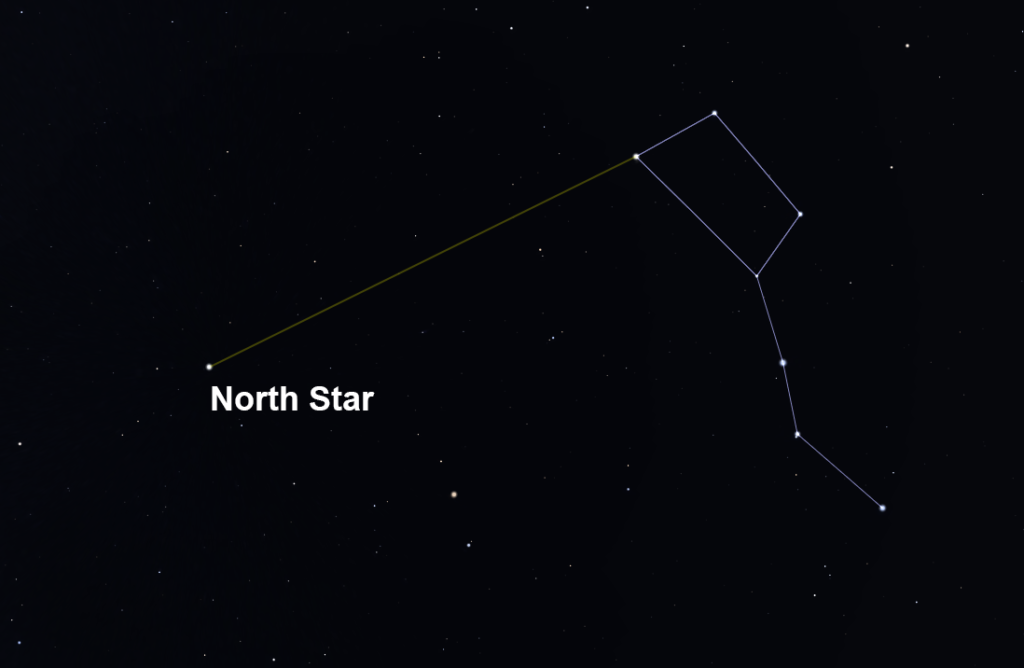
The North Star is almost directly over earth’s North Pole (within one degree). Therefore, on a round earth, the (angular) altitude of the North Star (its angular distance above the north horizon) is equal to your latitude (within one degree) – see figure 7. You can estimate the angular altitude of the north star using your hands. The width of your hand (with your fingers together) held at arm’s length covers approximately ten degrees. So turning my hand sideways and starting at the northern horizon, I can measure the number of hands it takes to reach the north star. Sure enough, it takes just under four hand widths, indicating the altitude of the North Star is just under 40 degrees as viewed from Colorado Springs.
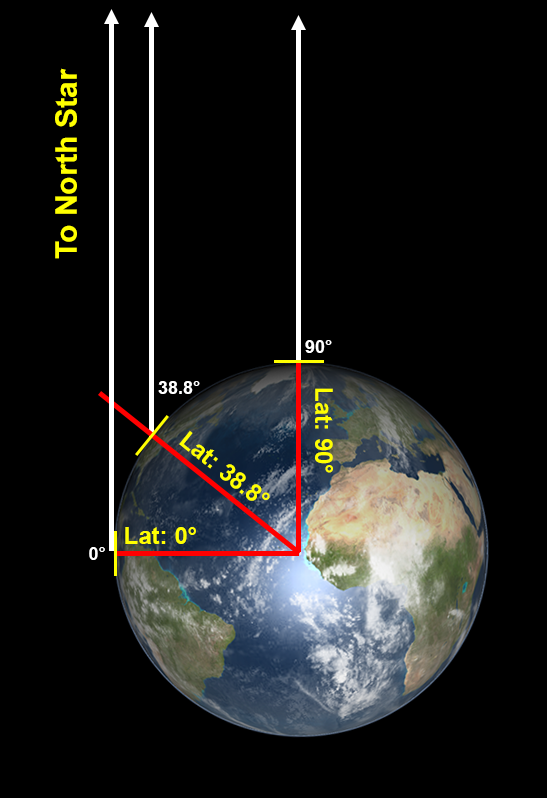
Honolulu has a latitude of 21.3 degrees. So it will take just over two hand widths to reach the North Star from there. The latitude of Fairbanks Alaska is 64.8 degrees. So it will take nearly six and a half hand widths to reach the North Star from the horizon. And from locations south of the equator, the latitude is negative, which means the North Star will not be visible. You can confirm that this works by checking the altitude of the North Star at your latitude, and have your friends at different latitudes check from their location (or travel there yourself). This works because the earth is round. But what happens if we assume a flat earth?
On a flat earth, the only way that the North Star could have a different (angular) altitude as seen from different latitudes is if it were relatively close to the earth – a few thousand miles above earth’s surface. And we know that the North Star is directly above earth’s north pole because it always appears due north from any location on earth (it must be in the center of the azimuthal equidistant projection map). From geometry, we can compute the distance of the North Star above the earth from our observations of the angular altitude of the North Star as viewed from various locations on earth.
We saw previously that there are 68.7 miles in one degree of latitude. So, take 90 degrees minus your latitude and multiply this result by 68.7 miles. This is your distance from the North Pole. On a flat earth, the distance of the North Star above the North Pole will be the tangent of its angular altitude multiplied by your distance to the North Pole. For Fairbanks, Alaska, this number is 3680 miles. In other words, if the earth were flat, then for the North Star to appear 64.8 degrees high from Fairbanks, its height would have to be 3680 miles.
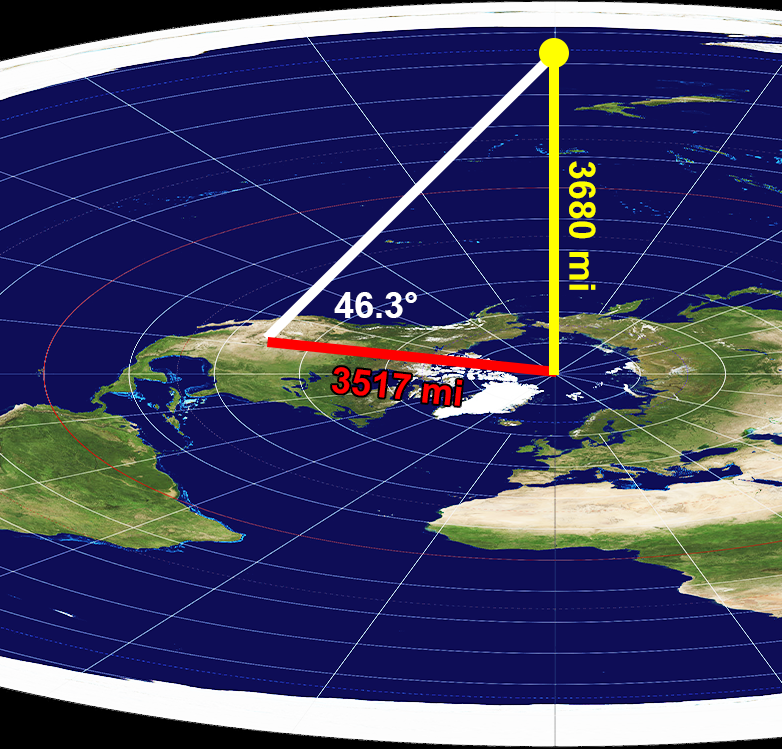
Using that distance, we can compute the angular altitude of the North Star from other locations on earth. On a flat disk, the angular altitude will be atan(3680 / ((90 – L)*68.7), where L is your latitude and “atan” means the inverse tangent or “arc-tangent.” So for Colorado Springs, the angular altitude of the North Star assuming a flat earth will be 46.3 degrees as illustrated in figure 8. But that isn’t the observed angular altitude of the North Star. I have measured it and found it to be very near 38.8 degrees, the same as the latitude of Colorado Springs. This matches the round earth prediction.
And for Honolulu, the altitude of the North Star should be 37.9 degrees if the earth were flat. But it isn’t. I have seen the North Star from Honolulu and can confirm its altitude at around 21.3 degrees. Moreover, the flat earth model predicts that the altitude of the North Star as seen from Sydney, Australia should be 23.4 degrees above the Northern horizon. But of course, the North Star cannot be seen from Australia because it is permanently below the horizon – which is only possible on a round earth.[5]
You could use a different distance of the North Star above the earth, but you will not find any value that will match the observations for more than one latitude. On a flat earth, everyone should be able to see the North Star substantially above the horizon, not just those people who live north of the equator. But observations rule this out. Geometrically, we know what the formula for the angular altitude of the North Star would be if the earth were flat, and it is not consistent with observations. It is simply impossible to both believe in a flat earth and also understand geometry.
Lunar Eclipses
One of the earliest evidences for a round earth, and one we can still use today, is a lunar eclipse. A lunar eclipse occurs when the earth passes directly between the sun and the moon. At such a time, the earth casts its shadow on the moon. And what is the shape of that shadow? It is a circle.
The earth is quite a bit larger than the moon, and even the earth’s shadow is larger than the moon at the distance of the moon. Consequently, you cannot see the entirety of earth’s shadow on the moon during a lunar eclipse. But you can see the perimeter of that shadow as the moon creeps across, and it is unquestionably a circle. Figure 9 is a picture I took of a lunar eclipse on November 8, 2003. Note the curvature of Earth’s shadow on the moon.

Could this possibly be consistent with a flat, disk-shaped earth? If the earth were a flat disk, then it would only cast a circular shadow upon the moon if the moon were directly over the North Pole at midnight. In any other configuration, it would cast an elliptical shadow, or even a straight line. But the moon is never directly over earth’s north pole, and lunar eclipses can happen at any time at night, not just midnight. In fact, the lunar eclipse shown in figure 9 took place at sunset from my location in Boulder, Colorado. As the sun was setting, the moon was rising and I was directly in between the two. If the earth were a flat disk, then the earth’s shadow on the moon should have been a straight line. But it was a circle instead. That only makes sense on a spherical planet.
Actually, in the modern flat earth model described above, lunar eclipses cannot happen at all. Recall that the modern flat earth model has the sun and moon always above the surface of the earth, each circling a point directly above the North Pole. If the moon and sun were always above the flat earth’s surface, then the earth could never be in between the sun and the moon, and could never cast its shadow on the moon. Some flat-earthers seem to realize this and claim that something else is causing the dark circle to move across the moon during a lunar eclipse. But what would that be? And why is it that modern astronomers can predict to the second when a lunar eclipse will occur by computing when the earth will be directly between the sun and the moon?
Mountains and Oceans
Those who live near mountains can easily demonstrate the curvature of the earth. In Colorado Springs, there are large mountains to the west, but the town itself and the land to the east are relatively flat except for the slight curvature of the earth. This causes a very interesting phenomenon at sunrise – a phenomenon that cannot occur on a flat earth.
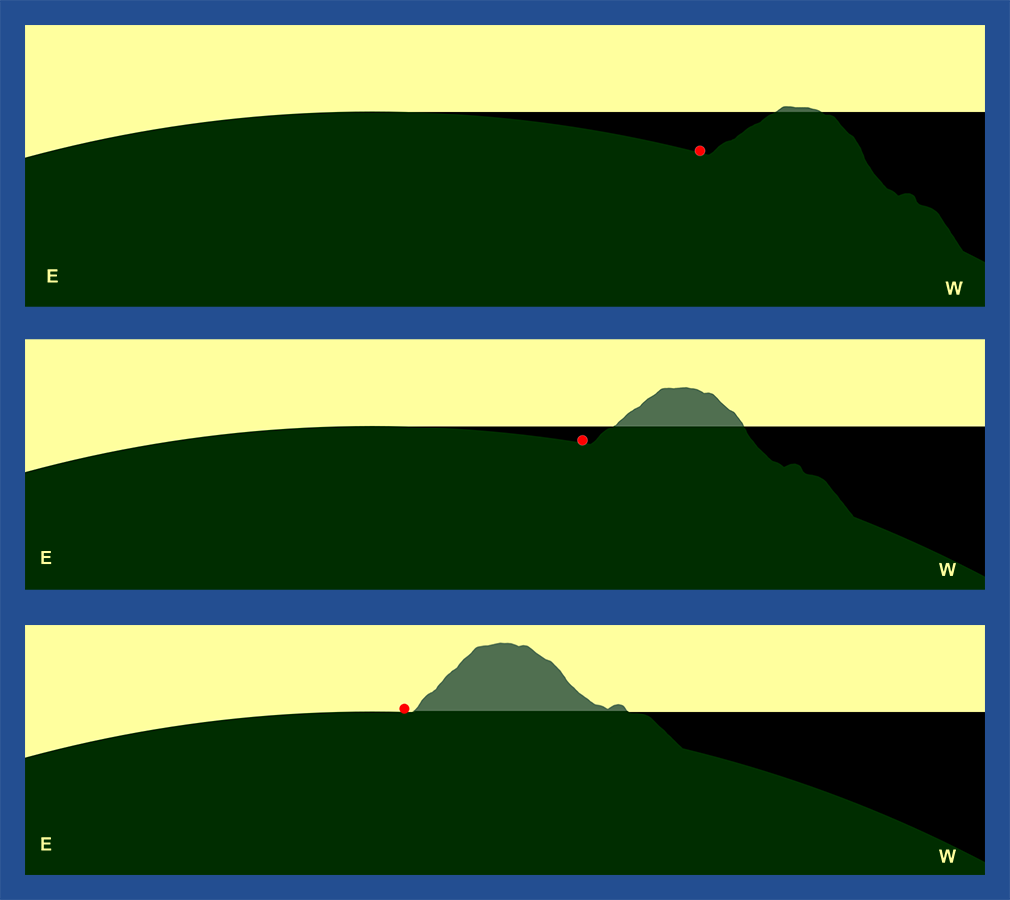
In the modern flat earth model, recall that the sun revolves around a point directly above the earth’s North Pole, moving from east to west, as seen in figure 3. Observers under the sun’s “spotlight” cone experience daylight. In this model, at the crack of dawn, who will receive sunlight first: an observer in the town of Colorado Springs, or the tops of the mountains to the west? Since the sun moves from east to west, its light cone will reach the town of Colorado Springs first, while the mountains are still in darkness. This is illustrated in the top frame of figure 10 which is looking south with the sun moving west. The red dot represents the town, and the yellow represents the cone of sunlight. In the first frame, observers in town can see the sunlight, but the mountains to the west are still in darkness. Only later will sunlight reach the base of the mountains, and drift upward as the light cone continues to drift westward, as shown in the second and third frame.

But on a round earth, the exact opposite occurs. On a round earth, the tops of the Rocky Mountains receive sunlight first because they are miles above the land to the east and therefore have a more distant horizon. This is shown in the top panel of figure 11. The sunlight is coming from the east, but the observers in the town are not able to see the sun because it is beyond their horizon. As the earth rotates, the tops of the mountains are illuminated first. Next, the middle portions are illuminated (middle panel) while the sun is still below the horizon for observers in the town of Colorado Springs. About the time the sunlight reaches the base of the mountains, those people living in town finally see the sun breach the eastern horizon, as shown in the bottom panel.
I have seen this myself and took photos to record the effect on October 3, 2018. At 6:56 a.m. Mountain Daylight Time, the tops of the mountains were illuminated by a beam of sunlight as shown in the top panel of figure 12. However the sun was still below my horizon at that time. Over the next few minutes, the beam of sunlight on the mountains gradually drifted downward like a curtain until it reached the base, at which point I could see the sun on the eastern horizon, as shown in figure 12. This can only happen on a round earth. On a flat earth, I would have seen the sun first, and the grassy field in the foreground would have been illuminated while the mountains were still in darkness.

The same type of phenomenon can be experienced at sunrise for those living on the east coast, or sunset for those on the west coast. Consider a tall condo at Myrtle Beach. As the sun rises, those people in the higher rooms can see the sun rise before those people on the beach. This is due to the curvature of the ocean, and would not be possible on a flat earth. By timing the difference in sunrise times at different heights, you can even calculate the size of the earth.
There are direct ways of measuring the curvature of the earth on the ocean and in locations that have very little relief in the terrain, such as western Kansas. The fact that you cannot see very far in a boat on the ocean (and that you can see farther from the crow’s nest than the deck) is only possible on a round planet, not a flat one. However, there are certain caveats that can complicate these kinds of measurements. Temperature differences in the air can cause light to refract (to bend) very slightly. The effect is negligible for the experiments we have previously discussed. But when looking along the surface of the earth, the effect can become substantial enough that you must include the effect of refraction in your calculation. Alternatively, you can make your observations on days in which the air temperature closely matches the ground temperature, which minimizes refraction.
A Round Sun and Moon
In the modern flat earth model, the sun and moon are also claimed to be flat disks rather than spheres. Perhaps this is because it would be hard to get a spotlight effect from a spherical sun? In any case, it is very easy to show that the sun and moon are spherical. For one thing, the sun rotates. As it does, features on its surface (such as sunspots) are carried long. It takes about 25 days for features near the equator to make a complete loop around the sun. I have equipment that allows me to safely view the sun and I have seen its rotation with my own eyes. I can see that sunspots move from across the surface day after day. Moreover, their angular speed is much faster when they are near the center than when they are near the limb. This can only be the case for a spherical sun, not a flat disk. The effect is even more pronounced when we view the sun in certain specific wavelengths, as shown here: https://vimeo.com/9640691
Likewise, the moon is clearly spherical and not a flat disk. There are many ways to demonstrate this. First, phases show the sphericity of the moon. Phases are caused by the angle between the sun and moon as seen by observers on earth. When the sun is to the right of the moon, the right side of the moon is illuminated by sunlight, and we see in the waxing phases. Conversely, when the sun is to the left of the moon, the left side of the moon is illuminated. You can simulate the phases of the moon by shining a flashlight on a golf ball and changing direction from the which the flashlight shines.

Furthermore, when we look at the moon through a telescope, the way the light falls on the craters clearly reveals that the moon is round and is being illuminated by the sun, as shown in figure 13. Flat-earthers believe that the moon is not illuminated by the sun, but produces its own light. But anyone with a telescope can see that this is not the case. The shadows in the craters show that the moon is illuminated by external light coming from the direction of the sun.
Finally, we can see the sphericity of the moon by observing it from different angles. The moon rotates at the same angular speed as its average revolution around the earth. For this reason, we always see (approximately) the same side of the moon. But beginning with the Apollo 8 mission, astronauts were able to photograph the moon from an angle that cannot be seen from earth – as shown in figure 14. Note that Mare Crisium (the large dark ellipse left of center) is always near the right limb of the moon as seen from earth (as in figure 13). But here we can see features far to the right that are never visible from earth.

Of course, conspiracy theorists will say that this is all photoshopped. But this photograph was taken decades before programs like Photoshop existed. The computer technology to map a flat disk onto a sphere and rotate that sphere simply did not exist at the time.

But more importantly, you can prove that the moon is a sphere if you have access to a small telescope and a camera. If you take pictures of the moon during different times of the year and carefully compare them, you will notice an effect called libration. This is the apparent oscillation (“wobble”) of the moon due to the fact that its rotation speed is constant, but its orbital speed around the earth varies slightly due to its elliptical orbit. For this reason, over time we can eventually see a bit more than 50% of the moon’s surface. Sometimes Mare Crisium looks very close to the limb, and other times it is a bit further in due to libration. By taking pictures roughly half a year apart to maximize the difference in libration at a given phase, placing them side by side, and crossing your eyes so that the red dots align, you can actually see the sphericity of the moon as shown in figure 15. Anyone with access to a small telescope can do this experiment.
Conclusions
There are many other proofs that the earth is round. And there are other (bad) arguments that flat-earthers use. For a more complete examination of these issues, please read Dr. Danny Faulkner’s excellent book: Falling Flat. This book is available in our web store.
I have noticed that those people who are firmly entrenched in the flat-earth movement cannot be reasoned with. They tend to be conspiracy theorists, and the problem with conspiracy theories is that evidence against them is assumed to be evidence for them. This is fundamentally irrational. And so this article is really not for them. It is for people who have heard flat-earth arguments and want to know if there is any substance to them. We have seen that there is not. We have seen here that (1) the Bible teaches a round earth and (2) the sphericity of the earth is scientifically provable from observations and trigonometry.
I understand that the shape of the earth is not a salvation issue as such. Christians are saved by God’s grace received through faith in Christ. Fortunately, God doesn’t require us to have a correct understanding of astronomy to be saved. Nonetheless, when professing Christians deny things that are directly observable in the present, it is dishonoring to the Lord and creates a stumbling block to evangelism. Why would an unbeliever be inclined to accept a Christian’s claims about Jesus if that Christian denies things that are directly observable and provable in the present? Hence, when Christians embrace flat-earthism, when they use fallacious arguments and bad hermeneutics to convince people of something that is false, this does have a strong negative impact on the spread of the Gospel.
Let us honor the Lord by being as truthful in all things as we can be. Of course, a round earth is not the only provable, observable fact that some professing Christians deny. Those of us who want God to be glorified in all aspects must stand against flat-earthism, and other errors in science or biblical interpretation. We have seen that some Christians deny that organisms with traits best suited to the environment are more likely to survive than others – the principle of natural selection. But what is the basis for such a denial? And how should Christians respond? More to come.
[1] https://www.flatearthdoctrine.com/flat-earth-scriptures/
[2] Columbus thought that it would be faster to reach the Indies by going West across the ocean than going all the way around Africa. Of course, the Americas were not yet known to the Europeans, and Columbus had underestimated the size of the earth.
[3] Usually, the Pacific Ocean is selected to be near the perimeter on such a map so that the land masses are less distorted.
[4] Recall, one degree in latitude is 68.7 miles.
[5] Flat-earthers agree that the North Star cannot be seen south of the equator, but they disagree on the reason. They argue that the star is too far away to be seen from that distance. But this is easy to disprove. For one thing, you can see from the surrounding constellations that the North Star is below the horizon for latitudes south of the equator. Flat-earthers seem to be unfamiliar with the shapes and positions of the constellations.

