Astronomy is the study of the physical universe beyond earth’s atmosphere. This includes objects like planets, nebulae, galaxies, moons, asteroids, comets, black holes, and, of course, stars. Stellar astronomy is the branch dealing specifically with stars – their distances, motions, compositions, and so on. Modern technology has allowed us to discover so much about the stars and to share that information quickly with the world. You can look up just about any star on the internet and find all kinds of fascinating information based on good science: its size, composition, luminosity, distance, coordinates, and so on. But you will also read information that is not accurate because it is based on antibiblical assumptions, such as the star’s estimated age and stage of evolution. Therefore, it is very useful to know something about the history of stellar astronomy to see how we know what we know, and to discern what we really know from what is merely claimed.
Stars Are Distant Suns
It is amazing to think that those little points of light we see in the night sky are the same type of object as our sun, many just as bright, and some are hundreds of thousands of times more luminous.[1] They appear tiny and much fainter than the sun because they are so much farther away. The sun is merely 93 million miles away from Earth.[2] The next closest star, Proxima Centauri, is 269,000 times farther away from Earth than the sun. So, it’s no surprise that stars look much fainter.
The idea that stars are suns is actually a fairly modern one. Most ancient cultures did not believe this. After all, it is not intuitive to think that a faint star might actually be as big and bright as the sun but millions of times more distant. So, how did we discover that stars are suns?
The first historical record of someone proposing that stars are like the sun goes to Anaxagorus from Athens around 450 B.C. He incorrectly believed that the sun was a hot rock. But he correctly believed that the moon was a rock that shines by reflecting sunlight. And he correctly believed that stars were the same kind of object as the sun. However, his ideas were considered heretical by the Greeks who believed that the sun was a god. Thus, his claims were not widely accepted.
Aristarchus of Samos (310-230 B.C.) revived the idea that stars are suns as a reasonable inference from his other discoveries. He correctly computed the distance to the moon using geometry and lunar eclipse observations, which allowed him to deduce the size of the moon relative to the earth. He also used geometry to compute the distance to the sun. Although his estimate of the sun’s distance was not very accurate due to the limitations of observations at the time, it was enough to show that the sun was much farther than the moon, and therefore much larger than the earth. This led Aristarchus to conclude that the earth must orbit the sun (heliocentrism), because he thought it would be ridiculous for the enormous sun to orbit the much smaller earth (geocentrism). That’s pretty insightful!
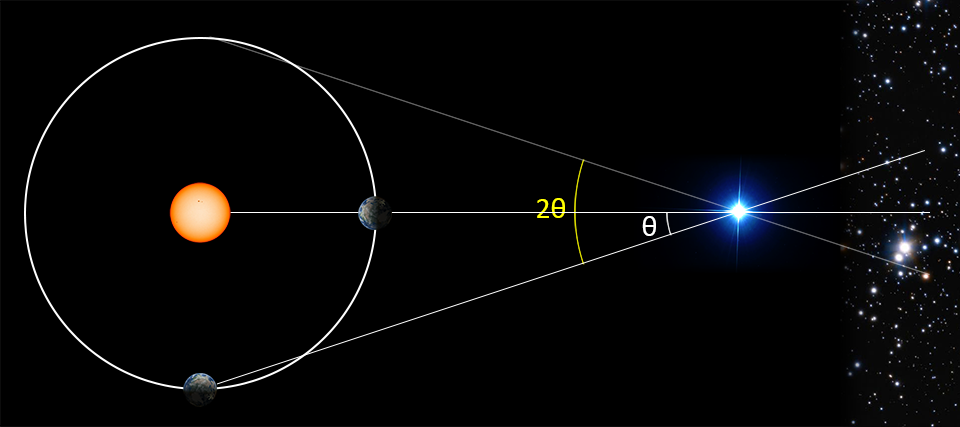
However, most other Greek scientists did not embrace the idea of heliocentrism and gave what seemed to be compelling evidence to the contrary. For example, if the earth orbits the sun, then why do we not feel an enormous wind? They also pointed out that if the earth orbits the sun, then nearby stars would appear to shift relative to more distant stars as the earth moves. This effect is called parallax. Parallax is defined as the shift in angle of a star as seen from earth at the two locations in the figure below. One location is when the earth is at a right angle relative to the star and the sun. The other location is when the earth is between the star and the sun. In practice, it is easier to compare the position of a star from when the earth is on opposite sides of the sun (perpendicular to the star’s position) and divide the angle by two to derive the parallax. This is the same method your brain uses to compute the approximate distance to an object based on the slightly different perspective between your left and right eye.
Yet, the constellations do not change shape throughout the year; we see no evidence of parallax. Geocentrists argued that this shows that the earth is not moving. Aristarchus correctly answered this objection by supposing that even the nearest stars are so far away that parallax would be too small to be seen by the unaided eye. At such a distance, stars would have to be as bright as the sun for us to see their light. Thus, stars are suns. Aristarchus was a brilliant man and well ahead of his time. But there were no telescopes at the time and hence no way to verify his suppositions. So, his correct ideas about the solar system were not embraced, and the Greeks and others continued to believe in a geocentric solar system for nearly two millennia.
Copernicus (A.D. 1473-1543) revived the idea of a heliocentric solar system. He pointed out that retrograde motion of the planets (the fact that outer planets seem to move backwards sometimes) would naturally be explained in a heliocentric solar system as the faster earth passes them. His ideas were published just before his death. They were controversial because the geocentric solar system of the Greeks was well accepted at the time.
The invention of the telescope in 1608 revolutionized the field of astronomy. Galileo’s observations beginning in 1610 strongly supported heliocentrism. He discovered four moons that orbit Jupiter – proving beyond all doubt that not everything orbits the earth. And his observations of the phases of Venus demonstrated that it must orbit the sun and not the earth. Johannes Kepler was a contemporary of Galileo and gave further evidence of the heliocentric solar system using data collected by Tycho Brahe. The heliocentric solar system was gradually accepted over the next century.
But still, there was no observable parallax. Even with the aid of telescopes, no one could detect the shifting of nearby stars relative to more distant ones as the earth orbits the sun. If indeed heliocentrism were true, then stars must be farther away than anyone had suspected.

The binary star 61 Cygni (the two brightest stars near the center) appears to shift relative to background stars in these two images taken seven months apart.
Finally, in 1838, mathematician and astronomer Friedrich Wilhelm Bessel became the first person to measure and publish the parallax of a star. He discovered that the star 61 Cygni had a parallax of roughly 1/3 of an arcsecond (one arcsecond is 1/3600 of a degree). This corresponds to a distance of about 10 light years, or 59 trillion miles. Astronomers often use the parsec to describe cosmic distances. The parsec is defined as the distance of a star whose parallax is 1 arcsecond. (Parallax of one second of arc = parsec). One parsec is equal to 3.26 light years which is about 19 trillion miles. The nearest star to the sun (Proxima Centauri) is 1.3 parsecs distant. The distance to a star in parsecs (D) is simply the reciprocal of its parallax in arcseconds (θ). D = 1/θ. For example, the bright star Sirius has a parallax of 0.37921 arcseconds, so its distance from the sun is 2.637 parsecs.

The nearest star to the sun is Proxima Centauri. It appears to jump back and forth relative to the more distance stars in these two images. One image is from the Earth and the other from the New Horizons spacecraft at about the same time. New Horizons was 4.4 billion miles (47 AU) away from Earth at the time, so the difference in perspective is striking.
Modern ground-based telescopes can measure a parallax as small as 0.01 arcsecond. Below that limit, the parallax is too small to be accurately measured due to the blurring effect of earth’s atmosphere. This limit corresponds to a distance of about 100 parsecs. The Hipparcos spacecraft (1989-1993) was able to measure much smaller parallax angles because it was above the earth’s atmosphere. It was able to measure stellar distances out to several hundred parsecs. The Gaia spacecraft was launched in 2013 and is still in operation. It can measure even smaller parallax angles and is therefore able to measure distances of stars up to 10,000 parsecs. Beyond these limits, astronomers must use other methods to measure the distance to a star.
Distances and Luminosities
Once the distance to a star is measured, the intrinsic luminosity of the star can be computed from its observed brightness. If you hold a lit candle one foot away from your face, it will appear quite bright. But the same candle a mile away would barely be visible even at night. This is apparent brightness – how bright something appears at a distance. But the luminosity of the candle did not change; it emits just as much light regardless of its distance from the observer. The amount of light that our eyes receive from the candle diminishes with distance.
The apparent brightness of an object is inversely proportional to the square of its distance from the observer. That is, if you double the distance to a candle, it will appear one fourth as bright. This geometrical principle allows astronomers to compute the true luminosity of any star if we know the distance to the star. We measure the apparent brightness using a photometer and then multiply by the square of the distance to determine the true, intrinsic brightness – its luminosity. Astronomers have performed such computations for many stars. These computations confirm that stars do have luminosities comparable to the sun.
The Magnitude System
The ancient Greeks had already developed a system for categorizing the apparent brightness of a star – how bright the star appears in our night sky. They divided stars into six classes of magnitude. The brightest stars of the night sky were said to be first magnitude. The faintest stars were sixth magnitude. This was a crude system because estimates were made by eye and were somewhat subjective.
Modern astronomers have modified and refined this system to make it objectively quantifiable. On our modern system, a magnitude difference of 5 is defined to be an apparent brightness ratio of 100. That is, a first magnitude star appears exactly 100 times brighter than a sixth magnitude star. For a difference of one magnitude, the ratio of apparent brightness is the fifth root of 100, which is approximately 2.512. On this modern system, the faintest stars visible to the unaided eye are still around magnitude 6, but the very brightest stars actually have a magnitude that is negative. Sirius (the brightest star in our night sky) is magnitude -1.46. The sun has a magnitude of -26.74.
The magnitude system is a bit counterintuitive to the uninitiated because it is “backward” and logarithmic. By “backward,” I mean that bright stars have a lower magnitude than fainter stars. And it is logarithmic in that a difference in magnitude between two stars corresponds to their brightness ratio and not brightness difference. This allows us to express an enormous range of brightnesses using relatively small numbers. The sun with magnitude -26.74 is brighter than a sixth magnitude star by a factor of 12.5 trillion![3]
The magnitude of a star refers to how bright it appears in the night sky. To emphasize this, we also refer to this as the apparent magnitude of a star. Apparent magnitude is symbolized by a lowercase letter m. But sometimes we want to examine the luminosity of a star – how bright it really is regardless of how bright it may look due to its distance. And it can be convenient to use the same “backward,” logarithmic system as apparent magnitudes. So, astronomers also use a system called absolute magnitude, symbolized by a capital M. By definition, the absolute magnitude of a star is the apparent magnitude it would have if it were exactly 10 parsecs away from us. Most stars are farther than this, so their apparent magnitude is greater (fainter) than their absolute magnitude. The sun has an absolute magnitude of 4.83. Since its apparent magnitude is much smaller (-26.74), this shows that the sun is much, much closer than 10 parsecs. (When the word magnitude is used without a prefix, apparent magnitude is implied.)
The relationship between apparent magnitude (m), absolute magnitude (M), and distance in parsecs (D) is simple: m – M = 5 log10(D/10). Since this equation has only three variables, you can always determine the third if you know the other two.[4] For nearby stars, we can use the measured parallax to determine the distance, and we can measure the apparent magnitude directly with a photometer. We then compute the absolute magnitude. However, there are certain kinds of stars whose absolute magnitude can be determined by other means. By measuring the apparent magnitude of these stars, we can compute the distance. This is one of the methods that works far beyond the limit of the parallax method.
Now that we know the distances to many stars by the parallax method, and measuring their apparent magnitude with detectors, we can compute the absolute magnitude corresponding to their true luminosity. We find that stars have a wide range of luminosities. But they are comparable to the sun because they are indeed suns. The faintest stars have a luminosity ten thousand times fainter than the sun, but the brightest stars have a luminosity of a million suns. Anaxagorus and Aristarchus were right: stars are just as bright as the sun, but they are at much greater distances. However, the fact that stars are as bright as the sun doesn’t mean that they are the same type of thing. How do we know what stars are made of, and do they have the same composition as the sun? We will explore this in the next article.
[1] With the exception of planets. Five of the bright points of light we see in the night sky are planets that are bright because they merely reflect sunlight as the earth does.
[2] On average.
[3] It is truly amazing that our eyes have such an astonishing range of brightness detection. We can see the sun during the day (do not stare!) and at night our same eyes can see stars that are 12.5 trillion times fainter than the sun!
[4] This ignores complications such as intragalactic extinction. Intervening material can cause a star to look a bit fainter than it would if the space between stars were completely empty. This effect is usually small but can be important in certain circumstances.