In the previous two articles, we discussed the conventionality of simultaneity. This is the counterintuitive principle that the synchronization of two clocks separated by a distance is a matter of convention, not an objective property of nature. And since any measurement of speed on a one-way journey requires the use of two synchronized clocks, there can be no objective one-way speed of light. Rather, it is a matter of convention. We may freely stipulate the speed of light in any one direction to be anything between ½c and infinity, and the return-trip speed is set by the constraint that the average speed of light must always be exactly c in vacuum (186,282.397 miles per second). We here explore additional objections to the conventionality thesis. These have all been refuted in the technical literature within the past century. But few people have access to such literature, and so a review is expedient.
Introduction and Review
The most common synchrony convention in use by physicists today is the Einstein synchrony convention (ESC). This convention stipulates that the one-way speed of light is exactly c in all directions – the same as the round-trip speed. This imposes a convenient symmetry and generally makes the mathematics of relativistic physics more tractable. However, it leads to some strange results. It implies that what we see happening now actually happened in the past. And how long in the past will depend on the state of motion of the observer. In other words, a supernova that we see today might have happened 4999 years ago according to Rachel, but happened 5012 years ago relative to Jeff, if Jeff and Rachel are at the same location but have different velocities.[1]
The most common synchrony convention used throughout history was the visual synchrony convention, also called the anisotropic synchrony convention (ASC). This stipulates that the one-way speed of light is infinite (or practically so) when the light is incoming, and ½c when the light is outgoing for any given observer. Light that is traveling perpendicular to an observer travels at speed c, the same as the average round-trip speed.[2] This system has the advantage that all events are observed in real-time; we see the universe as it is now. Furthermore, this is the only convention that does not require knowledge of the round-trip speed of light in order to know the timing of any celestial event. Hence, it was the only synchrony system possible in the ancient world.[3]
That we may simply stipulate the one-way speed of light in a given direction is deeply counterintuitive, probably because we tend to assume that time is universal and unaffected by motion. But Einstein found that this was not the case. Since most people have not had the opportunity to study Einstein’s discoveries, it is common for laymen to propose thought experiments that proport to measure the one-way speed of light without assuming any synchrony convention. But inevitably, there is always a catch. Either the experiment has tacitly assumed a synchrony convention, or it will yield the same results regardless of synchrony convention.
We saw in the previous article that the formula for time dilation given in most relativity textbooks is a simplified version based on the Einstein synchrony convention. The full time-dilation formula includes the Reichenbach epsilon, which reflects the choice of synchrony convention. Therefore, the degree of time-dilation for an object in motion will depend on the choice of synchrony convention. We found in the last chapter that time-dilation effects are generally (1) more severe under ASC than under ESC, and (2) have directional dependence under ASC, but not under ESC.
This is important because it explains why slow-clock transport cannot be used to synchronize clocks. Since there is directional dependence in time-dilation under ASC, a clock can lose one second when moved slowly from A to B and then gain one second when moved slowly from B back to A. The clocks are synchronized upon their reunion, but were not synchronized throughout the journey.
Furthermore, under ESC, there is no linear term in the formula for time-dilation, and therefore it can be ignored at slow speeds. Even at 14% the speed of light there is only 1% time dilation under ESC. But under ASC, there is a nearly linear dependence on velocity at low speeds, and hence it cannot be neglected even at slow speeds. Namely, at 1% the speed of light, an outward moving object experiences roughly 1% time dilation under ASC.
Rømer and Jupiter’s moons
The first successful measurement of the speed of light was performed in A.D. 1676 by the Danish astronomer Ole Rømer. At first, this experiment may seem to measure the one-way speed of light. But in fact, we will see that it is merely a variation on slow-clock transport. Hence, it tacitly presupposes ESC. Nonetheless, it did accurately measure the round-trip speed of light, despite the fact that the light used only made a one-way trip! How is this possible?
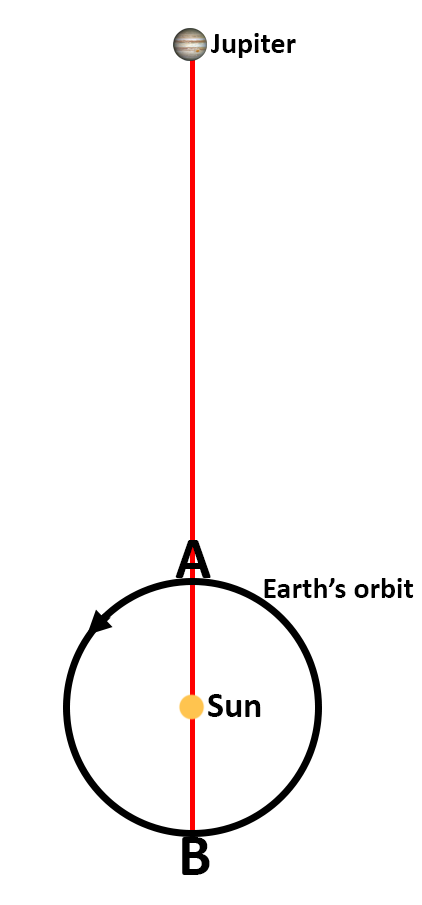
By the mid-1600s, astronomers were able to use geometry along with their observations of the positions of planets to calculate the approximate distance of each planet from the sun. The Earth orbits at an average distance of 93 million miles from the sun, whereas Jupiter orbits at about 475 million miles from the sun. Earth takes only one year to orbit the sun, whereas Jupiter takes 12 years.
When Earth and Jupiter are on the same side of the sun and aligned, (Earth is at point A in the figure) the two planets are only about 382 million miles apart (475 million miles minus 93 million miles). This event is called opposition because from our perspective on Earth, Jupiter is in the opposite direction in the sky as the sun.
But when Jupiter and Earth are on opposite sides of the sun, (Earth is at point B in the figure) they are farthest from each other – about 568 million miles. When this happens, Jupiter is said to be in conjunction. Of course, Jupiter is not easily seen from Earth at conjunction due to the glare from the sun. But Jupiter can be seen shortly before or after conjunction, where the distance is just a bit less than 568 million miles.
Furthermore, Jupiter has four large moons that can be observed in small Earth-based telescopes. Galileo discovered these in 1610. And by the time of Rømer, the periods of these moons were well known. The innermost moon, Io, takes 1 day, 18 hours, 27 minutes to orbit Jupiter. The precise timing was measured by noting when Io crossed directly in front of or behind Jupiter. Hence, Io acts like a clock.
But astronomers noticed that when Jupiter was near opposition (and hence closest to Earth), Io appeared to be a few minutes early. Furthermore, when Jupiter was near conjunction (and hence farthest from Earth), Io appeared to be a few minutes late. Rømer knew this, and speculated that a finite speed of light might be the cause.[4] Namely, when Jupiter was farther from Earth, perhaps Io merely appeared to be several minutes late because the light takes longer to traverse this greater distance.
By measuring the precise timing of Io, Rømer found that the “Io clock” was about 16.64 minutes behind schedule when Earth and Jupiter are farthest from each other than when they are closest to each other.[5] He supposed that the total difference of 16.64 minutes was how long it takes light to traverse the diameter of Earth’s orbit. And knowing that distance (186 million miles) and dividing that by 16.64 minutes, he correctly computed the speed of light.
Essentially, Rømer had measured the time it takes light to traverse the Earth’s orbit, from point A (where Earth is closest to Jupiter) to point B (where Earth is farthest from Jupiter). This would seem to be a one-way measurement of the speed of light. However, it unwittingly assumes ESC because it neglects the effects of time dilation. Namely, Rømer assumed that clocks on Earth are unaffected by the motion of Earth from point A to point B.
Now, under the ESC system, that is a good approximation. After all, Earth moves very slowly from point A to point B (slow compared to the speed of light) at an average speed of 18.5 miles per second. And under ESC, the effects of time dilation at such a speed are only about 0.0000005%, and therefore negligeable. Under ESC, clocks remain essentially synchronized during slow-clock transport.
But what happens when we analyze the situation under ASC? Clocks do not remain synchronized during slow-clock transport under ASC. But does the math produce the same answer? Let’s imagine a stationary observer at point B who is watching the Earth travel from point A to B. Jupiter is virtually stationary relative to this observer, and therefore clocks on Jupiter will tick at the same rate as the observer’s clock. But how will Earth clocks be affected by its motion toward this observer?
We use the full time-dilation equation presented in the previous article to compute this value. However, we can neglect the first term since it reduces to approximately 1 since v is so small compared to c. The time dilation will therefore be c/(c+v) where v is recessional velocity. We note that Earth changed its distance relative to our observer at point B by 186 million miles and did so over a time of six months for an average recessional velocity of -11.788 miles per second.[6] Putting this value into the formula, we see that Earth clocks tick 1.00006328 seconds for every one second of our observer’s clock (or a clock on Jupiter). So, Earth clocks are ticking fast, and over the course of six months, Earth clocks gain a total of 998.4 seconds. This is 16.64 minutes. That is exactly the time by which Io appears to be delayed according to Earth clocks.
So, under ASC, light takes no time at all to go from point A to point B. The reason Earth perceives Io to be delayed by 16.64 minutes is because Earth clocks are 16.64 minutes fast relative to clocks on Jupiter. So, whether the one-way speed of light is c or infinity, Io will appear to be delayed by 16.64 minutes when Earth and Jupiter are farthest apart. Since both conventions give the same result, Rømer’s observations are compatible with either convention. Hence, they cannot be used to establish the one-way speed of light.
Strangely, these observations do establish the round-trip speed of light. How is that possible? The reason is that time dilation depends on the one-way speed of light in exactly the same way as light travel-time. And therefore, it is impossible to observationally distinguish between the two. Do we see Io as 16.64 minutes late because of finite light travel-time, because our clocks have ticked fast, or some combination of the two? There is no way to know. We can see this in the mathematics:
Under slow clock transport, we may neglect the first term of the full time dilation formula, and so moving clocks tick at a rate of c/(c+v(2ε – 1)) where c is the round-trip speed of light and ε indicates the synchrony convention and hence the one-way speed of light. For negative velocities (v), the clock ticks slightly faster than its stationary counterpart, and it does so for a total time of r/v.
So a clock moving slowly (at velocity v) from A to B will experience a total time gain relative to stationary clocks of r(2ε – 1) / c where r is the distance between A and B.[7] And the time it takes light to cross from A to B is 2r(1- ε) /c. When we add these two terms, we get r/c which is the total time by which a clock at A (or at Jupiter) appears to be behind the clock at B. Notice that our answer (r/c) depends only on r (the distance between A and B), and c (the round-trip speed of light). There is no ε in the answer, and therefore the amount of time by which Io appears to lag does not depend on the one-way speed of light; it only depends on the round-trip speed of light.
Many physicists of the twentieth century have performed a similar analysis and rightly concluded that Rømer’s observations do not establish the one-way speed of light, but only the round-trip speed of light. Even Scott-Iveren who did not fully agree with Einstein’s relativity nonetheless noted in 1944 that “Rømer’s measurements and his method of calculation do not give the one-way velocity of light; they give only the there-and-back velocity.”[8] The Australian physicist Leo Karlov in 1970 published a detailed mathematical analysis of Rømer’s procedure, and showed that it does not refute the conventionality thesis. He states, “the method of Rømer (as indeed all observational methods of finding the speed of light) can only supply an objective average speed in a closed path.”[9] We have now seen why this is so: the effects of time dilation combine with the one-way speed of light so that only their combination is observable.
Maxwell’s Equations
Another objection to the conventionality thesis is that Maxwell’s equations supposedly require that the one-way speed of light is the same in all directions. Maxwell’s equations are four simple formulae upon which all electric and magnetic phenomena can be described. These equations show that a changing electric field will produce a magnetic field, and a changing magnetic field will produce an electric field. If the electric field changes in a sinusoidal fashion, it will produce a magnetic field that is also sinusoidal, which produces another electric field that is sinusoidal… and so on. The result is an electromagnetic wave that propagates through the vacuum of space at a speed of exactly c (the speed of light). This is no coincidence; light is an electromagnetic wave. But it wasn’t until Maxwell’s equations that we understood this.
I recognize that I lose a significant fraction of readers for every equation included in these articles. But you don’t need to know much about mathematics to understand why Maxwell’s equations only require the round-trip speed of light in vacuum to be c, but do not place any constraints on the one-way speed. There are two different ways of expressing Maxwell’s equations: the differential form and the integral form. They look like this:
| Integral Form | Differential Form |
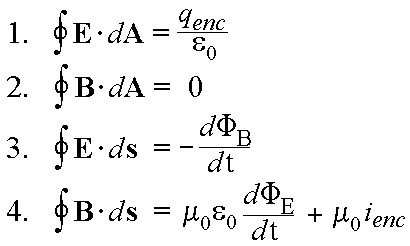 | 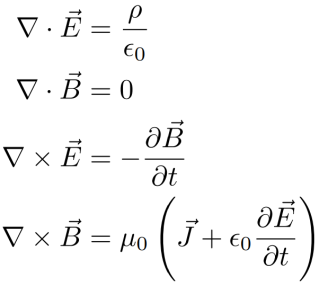 |
So, the equations on the left express the same physical truth as the equations on the right, but in a different form. Depending on the physics question, it may be easier to use the integral form, or the differential form. But both forms express the same underlying physics.
Notice that each of the equations in the left column begins with the symbol ![]() . This is a closed integral. It indicates that we are adding up infinitesimal values along a closed path or a closed surface. A closed path is one that ends at the same point it starts. In other words, it denotes a round-trip, not a one-way journey. All four of Maxwell’s equations in integral form have this closed integral. Therefore, they cannot be used to find the speed of light on a one-way trip – because they are integrating over a round-trip path.
. This is a closed integral. It indicates that we are adding up infinitesimal values along a closed path or a closed surface. A closed path is one that ends at the same point it starts. In other words, it denotes a round-trip, not a one-way journey. All four of Maxwell’s equations in integral form have this closed integral. Therefore, they cannot be used to find the speed of light on a one-way trip – because they are integrating over a round-trip path.
It’s not so obvious with the differential forms, but this is because they are actually a special case that assumes ESC. In 1978, Dr. Carlo Giannoni published a paper in which he derived the general differential form of Maxwell’s equations without synchrony assumptions.[10] The results show that electromagnetic waves can have different one-way speeds in various directions depending on the chosen Reichenbach epsilon. Therefore, the full synchrony-independent differential form of Maxwell’s equations does not require the one-way speed of light to be c, only the round-trip speed.
Aside from the mathematics, the history of science should demonstrate that Maxwell’s equations do not require the one-way speed of light in any particular direction to be c. Albert Einstein was well aware of Maxwell’s equations, and indeed they were the justification for his belief that the round-trip speed of light in vacuum was constant and exactly c in any reference frame. Yet Einstein believed that the one-way speed of light was a matter of convention. He did not appeal to Maxwell’s equations to justify his preferred choice of ε=1/2 because he understood that they only constrain the round-trip speed of light. Indeed, many physicists of the twentieth century have defended the conventionality thesis and yet were well aware of Maxwell’s equations.
Occam’s Razor
Sometimes people think that Occam’s razor establishes that the one-way speed of light is likely the same in all directions. Occam’s razor is the philosophy that when multiple scientific models correctly predict observable phenomena, the simplest model (that which makes the fewest assumptions) is preferred. This is a good philosophy and works well. Since any assumption we make can be wrong, the fewer assumptions we make, the less likely we are to be wrong. Hence, simpler models are likely to be more accurate than complex models if both models are equally compatible with observations. Some critics of the conventionality thesis have argued that having the one-way speed of light be the same in all directions is simpler (and therefore more likely to be correct) than having the one-way speed of light be different in different directions.
The problem here is that Occam’s razor is about choosing between competing scientific models – not conventions of measurement. In other words, the statement “the one-way speed of light is the same in all directions” is not a hypothesis about the nature of light, but a stipulation that I make in order to define what constitutes “simultaneous” events separated by some distance. By choosing the one-way speed of light, I am defining a coordinate system. I am not making any objective claim about the nature of the universe.
In this sense, synchrony conventions are like any other system of measurement. We can measure lengths using inches, feet, yards, meters, or centimeters. Each of these is equally appropriate and it doesn’t make sense to say that one unit is more correct than any other. The metric system is certainly simpler than the Imperial system, but we wouldn’t appeal to Occam’s razor to argue that the metric system is more likely to be true than the Imperial system. It doesn’t even make sense to talk about a system of measurement being “true” or “false” because such systems are defined, not discovered.
The metric system is often more convenient than the Imperial system. But its simplicity cannot be taken to be more likely to be true than the Imperial system by Occam’s razor because these are not competing models. Nature does not prefer one system over the other. They are defined, conventional, systems of measurement by which we assign numbers to physical properties. The numbers we assign will depend on the convention, but conventions are not true or false. They are definitions that allow us to quantify aspects of the universe. And we can always convert from one system to another, e.g. 2.54 cm = 1 inch.
Likewise, the one-way speed of light is simply a humanly stipulated choice by which we designate what “simultaneous” means for two objects separated by some distance. Such a choice defines a coordinate system by which we assign numbers (x,y,z,t) to any event in spacetime. And we can convert from one system such as ESC to another system such as ASC, just as we can convert from metric to Imperial. The numbers that result will differ, but the underlying reality is the same.
Consequently, anyone arguing that one synchrony convention is more likely to be true than another on the basis of Occam’s razor does not understand what a synchrony convention is. A synchrony convention is a coordinate system. It allows us to assign three spatial and one temporal quantity to any event in spacetime.
Conclusion
The search for an objective, synchrony-independent method of measuring the one-way speed of light is futile. This is because to measure any one-way speed requires a synchrony convention, and hence a stipulation of the one-way speed of light. The most common methods of attempting to circumvent this difficulty inevitably fail. They generally rely upon slow-clock transport, and tacitly assume ESC. Or, they rely upon a signal transmission, but such transmissions subtly depend on the one-way speed of light. Maxwell’s equations do not settle the issue either because they only determine the round-trip speed of light in vacuum. Nor can Occam’s razor be applied since it distinguishes between models, not conventions. The visual synchrony convention (ASC) is therefore just as legitimate as the more recent ESC system. And since the visual synchrony system was the only one available in the ancient world, we have every reason to believe that the Bible uses this system. By this system, we are seeing stars in real time. And there is no distant starlight problem. There never has been.
[1] However, ESC does have the advantage that all observers with the exact same velocity (both speed and direction) will agree on whether two clocks are synchronized regardless of the position of those observers. In other words, ESC is a velocity-based convention.
[2] For the mathematically inquisitive reader, the one-way speed of light when not directly incoming is given by the formula: c/(1-cos(θ)), where c is the round-trip average speed of light, and θ is the angle of departure from directly inward. So θ=0 for directly incoming light and θ=180° for directly outgoing light.
[3] ASC has the advantage that all observers with a common position will agree on whether two clocks are synchronized, regardless of their velocity. ASC is therefore a position-based convention.
[4] Another possible explanation is time dilation. Namely, Earth’s clocks do not tick at a constant rate relative to Jupiter’s clocks, due to their relative motion. But no one knew about time dilation in the 1600s.
[5] Here, we will use the modern known values which are more accurate than what was possible in Rømer’s time.
[6] Note the “v” in the second term of the time dilation formula is defined as velocity away from the observer. Since Earth is moving toward the observer, this velocity is negative. And since this v is the recessional velocity, we consider only velocity that is radial compared to our observer, and not tangential to his line of sight. Effectively, we treat the Earth as if it had moved directly from A to B in a straight line, rather than along a curved path. Using the curved path will produce the same answer, but involves calculus.
[7] Since this is for slow clock transport, we have taken the limit as v approaches zero.
[8] P. A. Scott-Iversen, Introductory notes on a reformulation of the special theory of relativity, Philosophical Magazine 35, 105–120 (1944).
[9] Karlov, Leo, Does Roemer’s method yield a unidirectional speed of light?, Australian Journal of Physics 23, 243–258 (1970).
[10] Giannoni, Carlo, Relativistic Mechanics and Electrodynamics without One-Way Velocity Assumptions, Philosophy of Science, Vol 45., No. 1, March 1978, pp. 17-46.

