Although distant starlight has been used as an argument against the biblical timescale, we saw previously that the time it takes light to travel on a one-way journey is not a universal or objective value, but depends on how we define ‘simultaneous.’ Under the visual synchrony convention, we are seeing the universe in real-time. And since the Bible apparently uses this ancient convention, there is no starlight problem. If you haven’t read the previous article in the series, be sure to do so before continuing because this article builds on what we covered there. We will here investigate common objections to the conventionality thesis[1] – the principle that the one-way speed of light cannot be measured but is instead stipulated.
By way of review, the average round-trip speed of light in vacuum is always exactly c (186,282.397 miles per second). However, we are free to define the speed of light on a one-way trip, and this constitutes a definition of simultaneity for a given observer. That is, it allows him to judge whether two events at different locations happened at the same time.
In order to measure any one-way speed, we require two clocks separated by some distance. The first clock is at the starting point and records the start time of the object whose speed is to be measured. The second clock is at the finish line and records the arrival time. By subtracting the start time from the arrival time, we obtain the total time of the journey. The distance between the clocks divided by the time yields the one-way speed. However, this technique only works if the two clocks are synchronized (if they read the same time at the same time). But we found previously that “at the same time” is not objective – it depends on the frame of the observer and the one-way speed of light.
Hence, to ensure that two clocks (separated by some distance) are exactly synchronized, we would have to already know the one-way speed of light. And to measure the one-way speed of light would require to clocks separated by some distance that are exactly synchronized. Each question requires knowing the answer to the other one first. Consequently, there can be no objective answer to either question.
Albert Einstein recognized that this situation indicates that the one-way speed of light is not an objective quantity that is determined by nature. Rather, it is conventional. We may actually choose the one-way speed of light in any given direction because the speed of light can only be objectively measured as an average value on a round-trip, as in from A to B and back to A. The speed of light on a one-way trip (as in from A to B) cannot be objectively measured, but is instead stipulated. This is deeply counterintuitive because we tend to think of the passage of time as universal and independent of motion. But Einstein showed that this is not the case. He discovered the relativity of simultaneity, from which we can logically deduce the conventionality thesis, as we saw in the previous article.
Background
Since the conventionality thesis is so contrary to our intuitive expectation of absolute time, many people have proposed hypothetical experiments that they think will objectively measure the one-way speed of light. However, in all cases, these experiments will yield the same result regardless of the one-way speed of light, and therefore cannot actually distinguish different values of one-way speeds. There is always something that has been overlooked.
In fact, some physicists of the early twentieth century invented thought experiments that they believed could objectively measure the one-way speed of light, and published these in the technical literature. Some of these were attempts to disprove Einstein’s newly discovered physics of relativity. However, inevitably, these thought experiments were refuted by other physicists in subsequent publications. The refutations always revealed either a hidden assumption, or the fact that alternate synchrony conventions produce an identical outcome. Indeed, there is a rich body of technical literature on the conventionality thesis. But many laymen do not have easy access to such literature. So, we will here examine the two primary attempts to measure the one-way speed of light, and show why they fail.[2] All thought experiments ever proposed are some variation of these two methods; therefore, if they are disproved then so are all the others. I emphasize that the methods described here have already been disproved (in many cases over a century ago) in the technical literature. So, if someone repeats such a claim today, he reveals that he has not read the literature. But first, some terminology is in order.

Suppose we have two clocks at locations A and B respectively, located along the x axis with B to the right of A. The clock at A emits a light pulse at time t1. The light arrives at the clock at B at time t2, and is reflected back to A. The clock at A records the final arrival time at t3. To make the math easier, let’s suppose the two clocks are separated by a distance of 186,282.397 miles, and that t1 = noon. In such a case, t3 will be exactly two seconds past noon, because the time the light takes to go from A to B and back to A will be exactly two seconds: (t3 – t1 = 2 seconds). This experiment will confirm that indeed the round-trip speed of light (in vacuum) is exactly c, which is 186,282.397 miles per second. The question then is, “what is the time (t2) the light arrived at the clock at B?” That will depend on the chosen synchrony convention and is expressed by this formula:
t2 = t1 + ε(t3 – t1), (0 ≤ ε ≤ 1)
Here, the variable represented by the Greek letter epsilon (ε) is called the Reichenbach epsilon.[3] It represents the chosen synchrony convention and can have a value of anywhere between zero and one. Einstein preferred to set the value to ½, and most physicists also prefer this value because it usually makes the math easier. Setting the Reichenbach epsilon to ½ is equivalent to setting the one-way speed of light to be the same in the positive x direction as in the negative x direction. This is called the Einstein synchrony convention (ESC). Under ESC, you can confirm using the above formula that the light arrives at clock B at time t2 = 12:00:01, exactly one second past noon.
Previously, we discussed the visual synchrony convention in which light traveling directly toward the observer is instantaneous and light traveling directly away travels at ½c. Since the one-way speed of light is different in different directions, this is an anisotropic synchrony convention (ASC). Under ASC, the Reichenbach epsilon can be either zero or one depending on where the observer is. Let’s suppose that the observer is far to the left of clock A. In this case the Reichenbach epsilon is equal to 1. Plugging this value into the above formula (ε = 1), you can see that t2 = t3 under the ASC convention. That is, the light reaches clock B at exactly 12:00:02, and is reflected back to clock A which it reaches immediately at 12:00:02. Therefore, light moves from A to B at ½c (because it is outgoing), and moves instantly from B back to A (because it is incoming relative to the observer).
So, under ESC, clock B is synchronized with clock A if it reads 12:00:01 when the light arrives. But under ASC, clock B is synchronized with clock A if it reads 12:00:02 when the light arrives. Our choice of synchrony convention, and thus our choice of ε will determine how we synchronize these two clocks. Then when we use our synchronized clocks to measure the one-way speed of light, the answer will be whatever we chose at the start. Choosing a synchrony convention is the same as choosing the one-way speed of light. And choosing the one-way speed of light is the same as choosing a synchrony convention.
With this background information, we can begin examining the thought experiments that attempt to objectively measure the one-way speed of light without first stipulating it (or equivalently stipulating the synchrony convention). We will find that in all cases, such methods subtly assume the one-way speed of light as part of their setup, thereby invalidating the results. Virtually all thought experiments that attempt to objectively synchronize two clocks separated by a distance will fall into one of two categories: signal synchronization, and clock transport. We begin with the first.
Signal Synchronization
One of the simplest methods is to use a signal, such as a radio pulse, to synchronize the two clocks. Suppose at exactly noon, a radio transmitter at clock A emits a pulse that travels to B. Upon reception of that signal, clock B is set to noon. Then the two clocks are supposed to be synchronized. But are they?
That would certainly be the case if radio transmissions were instantaneous. But in fact, we know from many experiments that the round-trip speed of radio in vacuum is exactly the speed of light.[4] But we don’t know radio’s one-way speed because we don’t know the one-way speed of light. We could assume that the one-way speed of radio (and therefore the one-way speed of light) is the same (c) in any direction. Then it would take the radio pulse one second to arrive at clock B, and we should set clock B to one second past noon when it receives this light. If we then used these two clocks to measure a light pulse from A to B, we would find it takes one second to traverse the distance, implying that the one-way speed of light from A to B is exactly c. But then again, that is the very thing we assumed when we synchronized clock B with clock A under the assumption that radio (and therefore light) travels at a one-way speed of c. This begs the question. So, this experiment cannot objectively measure the one-way speed of light without first assuming it.
Some people have suggested that placing the radio transmitter exactly in between A and B would solve the problem. The radio transmitter emits a pulse (in both directions) at noon. The pulse travels to A and to B, and they set themselves to noon upon receiving the pulse. Sure, their time may be a bit behind the clock at the radio transmitter, but at least they will apparently be synchronized with each other; and that is all that is required to measure a one-way speed.
But in assuming that the light from the radio transmitter arrives at A at the same time it arrives at B assumes that the one-way speed of radio (and hence the one-way speed of light) is the same in opposite directions. So, this method assumes the Einstein synchrony convention at the start. But suppose we use the ASC system instead. Then light from the radio transmitter will reach A instantly (since it is incoming relative to the observer far to the left), and will reach B one second later (since it travels at ½ c for a distance of ½ of 186,282.397 miles). If the clock at B is set to noon when the light arrives, then it will be one second behind A, and is therefore not synchronized. So, under ASC, we should set the clock at B to one second past noon when it receives the light in order for it to be synchronized with clock A. If we then use these synchronized clocks to measure the one-way speed of light, we will find light takes two seconds to go from A to B, and no time at all to go from B to A. But that of course is what we assumed when we agreed to use the ASC convention.
Clearly, we cannot use light or radio or any electromagnetic radiation to synchronize these two clocks because we would have to first know the one-way speed of light in order to know when the signal arrived at each clock. And that is the very thing we are attempting to objectively measure. What about electricity? We could have a long wire running from A to B, and send an electric pulse when clock A reaches noon. Upon receiving the electric signal, clock B is also set to noon. Are the two clocks now synchronized?
By now you might realize that there is always a catch. And indeed, there is. Electricity actually travels at the speed of light. And so, this suffers the same problem as using a radio pulse. When the electric signal arrives at B, should we set clock B to noon, to 12:00:01, or to 12:00:02? Whatever value we pick amounts to choosing the value for ε, which means we have already assumed the one-way speed of light in synchronizing these clocks. Clearly, we need a signal that does not depend on the speed of light.
Suppose we manufacture a long, rigid, copper rod that is exactly 186,282.397 miles in length. One end of the rod is at A and the other end is at B. When clock A strikes noon, we push on the rod. When the clock at B feels the rod move, it sets itself to noon. Are the two clocks now synchronized? After all, experience tells us that when you push on one end of a rod, the other end moves instantly. Or does it?
In fact, when you push on one end of a rod, you are pushing on the atoms at the end, which then push on the atoms next to them which do the same and so on; it’s essentially a domino effect. This creates a compressional wave that travels down the rod until it reaches the other end. It may seem like the other end moves instantly, but it doesn’t. The compression wave actually travels at the speed of sound in the material, which is generally far slower than the speed of light. At room temperature the speed of sound in copper is 4760 meters per second (about 2.958 miles per second). That’s a snail’s pace compared to light. So, the clock at B would feel the pulse about 17 hours, 30 minutes after noon.
Still, if we knew the exact speed of sound in copper (or whatever material we choose), we could compensate by setting the clock at B forward by the appropriate amount, e.g. 17.5 hours after noon. But that number is approximate. To measure the one-way speed of light, we need the clocks at A and B to be exactly synchronized since even a one second offset is the difference between the one-way speed of light being c and infinity. So we would need to know the exact speed of sound in the material.
In principle, we could measure the speed of sound in copper with extremely high precision using our long copper rod. When clock B feels the pulse at about 17.5 hours after noon, it instantly pushes back on the rod sending a compressional wave toward the clock at A. The clock at A will receive this pulse after another 17.5 hours. Dividing the total distance by the total time gives the speed of sound in copper. For the sake of simplicity, let’s suppose the times are such that this speed turns out to be exactly 4760 m/s. Knowing this speed, we compute how long it takes the pulse to travel from A to B: precisely 17 hours, 29 minutes, 41.6 seconds. Therefore, clock B should set itself to 5:29:41.6 a.m. upon receiving the pulse. And we suppose the two clocks are now exactly synchronized.
But have we made an untested assumption? Our method of measuring the speed of sound in copper actually measured its average speed on a round-trip. In other words, we have assumed that the speed of sound in copper is the same going from A to B as it is from B to A. There is good evidence that the speed of sound in copper is approximately the same in opposite directions.[5] But in order for this method to work, that speed would have to be exactly the same, or at least we would have to know its difference.
The reason sound moves through a substance is because atoms collide with neighboring atoms. But the way atoms “feel” each other is due to electromagnetic forces. Atoms are made of charged particles, including a cloud of surrounding electrons. These electrons repel the electrons of other atoms by their electric force. But that force is not transmitted instantly. Electric forces travel at… (wait for it) … the speed of light. Therefore, if the speed of light is different from A to B than it is from B to A, then the speed of sound in a substance like copper will also be (very slightly) different in different directions. Under ASC, this speed will be very slightly faster in the incoming direction than in the outgoing direction. For example, under ASC, the sound pulse in the rod will take 17 hours, 29 minutes, and 42.6 seconds to go from A to B, but only 17 hours, 29 minutes, and 40.6 seconds to travel back to A.
So, under the ASC convention, the clock at B should be set to 5:29:42.6 a.m. upon receiving the pulse in order to be synchronized with A. If we do this and then measure the one-way speed of light, we will find that it is indeed ½c from A to B, and instantaneous from B to A. So, again, the way in which we synchronize clocks depends on our previous choice of ε, which is the same as choosing the one-way speed of light.
It would seem that the two clocks separated by a distance cannot be exactly synchronized by signal transmission without first assuming the one-way speed of light. This is because all signals depend at least slightly on the one-way speed of light. Approximate synchronization is good enough for measuring the (approximate) one-way speeds of phenomena that are slow compared to light. But for light, the clocks at A and B must be exactly synchronized, since even a one second difference will drastically affect the result. And there is no way to do that by signals since all signals depend in some fashion on the one-way speed of light.
If there were some signaling method that did not depend in any way upon the speed of light, then perhaps synchronization by signal transmission would be possible. Two such methods have been proposed. The first is the use of tachyons. Tachyons are hypothetical particles that travel faster than light. In fact, in the limit as a tachyon’s energy goes to zero, its speed goes to infinity. So, if tachyons can carry information, then in principle tachyons would allow for instantaneous communication in opposite directions. It would seem that we could synchronize two clocks exactly by using instantaneous tachyons.
But there is always a catch. First, tachyons apparently do not exist. In fact, there are good reasons to think that information-bearing tachyons cannot exist – they would violate causality. In other words, tachyons that move forward in time in one reference frame, would be moving backward in time in another reference frame. In principle you could use tachyons to affect the past. This leads to temporal paradoxes. For more details, see the Physics of Einstein.
The second problem is that tachyons that are claimed by one observer to be instantaneous would not appear as instantaneous to another observer in a different velocity frame. This is due to the relativity of simultaneity as discussed in the previous article. Our measurement of the one-way speed of a tachyon will depend on the chosen synchrony convention, and hence our choice of the one-way speed of light.
The second method sometimes proposed is to synchronize two clocks using quantum entanglement. Quantum entanglement is a very strange aspect of quantum physics involving two particles that have interacted with each other in the past. Such interaction causes the particles to become entangled, such that even when the particles are separated by an enormous distance, they can subtly influence each other – and they can do so instantaneously. In particular, there is evidence that unobserved particles behave as waves, extended over a volume of space. Observing the particle “collapses the wavefunction” thereby making the wave behavior cease. But it also collapses the wavefunction of its quantum-entangled partner. And it does so instantaneously, regardless of the distance between the two particles.
The problem is that quantum entanglement cannot be used to send information instantly from A to B. We can’t actually observe a particle’s wavefunction, and therefore we cannot know the exact time that the wavefunction collapsed. We can confirm after the fact that the observation of a particle at A did indeed collapse the wavefunction of the particle at B. But the relative times cannot be known. Therefore, there is no way to use this information to synchronize two clocks at different locations.
Slow Clock Transport
If we cannot synchronize the clocks while they are separated with a signal transmission, perhaps we can synchronize them when they are together, and then move them to separate locations. So, we bring the clock at B to the location of A and synchronize them. We can conclude that they are truly synchronized if they read identical times. This is because however long the light took to reach our eyes from one clock, it took the same time from the other clock since they are at the same position. Therefore, if two clocks at the same location look synchronized then they truly are synchronized.
So, we then move one of the clocks to location B, confident that they are now synchronized. But are they? Einstein discovered that motion affects the passage of time, and hence the rate at which clocks tick. The very act of moving the clock to B causes it to tick at a slightly different rate along its journey than the clock at A ticks. Hence, when the clock reaches B, it is no longer synchronized with the clock at A.
There are two ways we might attempt to alleviate this difficulty. First, Einstein discovered the mathematical formula that describes exactly how time is affected by motion. So, by knowing the exact velocity of the clock as it is moved to B, we can use the formula to compute how much time was affected, and can then adjust the clock at B accordingly. However, the full version of this formula includes the one-way speed of light – the very thing we are attempting to measure. We would have to choose the one-way speed of light in order to use the formula, which obviously begs the question.
Second, the rate at which time is affected by motion is strongly dependent on velocity. Moving a clock very rapidly causes it to rapidly become desynchronized with its stationary counterpart. But moving a clock very slowly causes it to only slowly become desynchronized. What if we moved the clock to B as slowly as possible? Would it then still be synchronized with the clock at A?
Suppose we synchronize the two clocks at location A, then rapidly move one of them to B and then back to A. Einstein’s formula shows that the clock that moved will be behind the clock at A by some amount.[6] The faster you move the clock on its round-trip journey, the more it will lag behind the stationary clock. We don’t notice this effect in our daily lives because it is so small at the slow speeds we normally experience. But it has been measured on high-speed aircraft using atomic clocks. The effect is real.
This effect becomes vanishingly small as the speed (at which we move the clock from A to B and back to A) approaches zero. In other words, if we moved the clock from A to B and then back to A as slowly as possible, it will still be synchronized with the clock at A upon its return.[7]
So, slow speeds seem to be the key to retaining synchronized clocks. Therefore, people have proposed the following method for synchronizing two clocks separated by a distance. First synchronize the two clocks at the same location A. Then move one clock to B as slowly as possible. The assumption is that the two clocks are still synchronized. After all, if we move the clock at B back to A as slowly as possible, it will still be synchronized with A.
This method is called slow clock transport. And it seems reasonable at first. But by now, we know there is always a hidden assumption. Yes, under slow clock transport, you can move a clock slowly to B and back to A and they will still be synchronized upon their reunion. But how do you know that the two clocks remained synchronized throughout the journey? In other words, what if the moving clock loses one second as it is moved to B, and then gains one second as it is moved back to A? In fact, under ASC, this is exactly what happens.
Again, people might ask, “why would the effect of motion on the passage of time be different in different directions?” But the effect of motion on the passage of time is related to the speed of light. Therefore, if the one-way speed of light is different in opposite directions, then so will the effects of motion on the passage of time. The two effects are intimately connected. Thus, to arbitrarily assume that time dilation has no directional dependence is the same as assuming that the one-way speed of light has no directional dependence.
Again, some people think the solution is to put both clocks exactly in between A and B, and synchronize them at that location. Then one clock is moved (very slowly) to A while the other is moved (very slowly) to B at an equal speed. It is assumed that any time dilation they experience would be the same since they moved at the same speed. But that is only the case under ESC. Under ASC, time-dilation has a directional dependence. Therefore, to assume that two clocks are synchronized using slow-clock transport is to assume ESC at the outset – they very thing we are supposed to be testing. Hopefully you can now see why slow clock transport cannot objectively measure the one-way speed of light without first assuming it.
Let’s have a quick look at the mathematics of this. Let t represent the time between two events at the same location as measured by a stationary clock, and t′ (pronounced “tee prime”) represent the time between those same two events as measured by a clock moving in the positive x direction at speed v. As always, c represents the round-trip average speed of light in vacuum. Then the formula for time dilation as listed in most textbooks on relativity is:
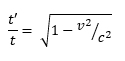
So, if the clock moves at 50% the speed of light, then v/c = 0.5, and t′/t = 0.866. At such a speed, the moving clock ticks slower than the stationary clock. It experiences only 0.866 seconds for every one second experienced by the stationary clock. But this formula is simplified; it is based on the Einstein synchrony convention. Since most physicists work almost exclusively in the ESC system, this is the formula they would use. However, if we are attempting to test between different synchrony conventions, then we cannot use this simplified form since it assumes ESC. Fortunately, the full formula for time-dilation without assuming any synchrony convention was derived by John Winnie in 1970.[8],[9] It is the following:
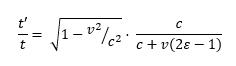
You can see that the full formula is basically the simplified formula multiplied by a term that contains the Reichenbach epsilon in the denominator. Notice that when the Reichenbach epsilon is set to ½ (as it would be in ESC), then the “extra” term on the right reduces to 1, and hence disappears, resulting in the simplified formula found in most textbooks. Under the ASC convention, ε = 1. So, under ASC, a clock moving in the positive x direction at 50% the speed of light would experience time dilation of: t′/t = 0.5774. Apparently, the moving clock ticks substantially slower at a given speed under the ASC convention than it does under the ESC convention. In most situations, time dilation effects are more severe under ASC than under ESC. Also, under ASC, clocks moving toward the observer can actually experience time contraction; they can tick faster than the stationary clock. This effect does not occur under the Einstein synchrony convention.
Under slow clock transport, the speed of the clock is much less than then speed of light. That is v/c is very small. And when you take the square of a number much less than 1, you get an even smaller number. So, v2/c2 is very, very tiny, and hence negligible.[10] Therefore, the left-hand term in the formula reduces to 1 in slow clock transport. But the right-hand term remains.[11] Of course, in the simplified formula based on ESC, there is no right-hand term, and so the entire formula reduces to 1. Therefore, the effects of time-dilation are negligible in slow-clock transport using ESC. But they are not negligible under ASC due to the linear v term in the denominator.
So, if we synchronize both clocks at A, and move one of them to B very slowly, how much time will be gained or lost? Under ESC, the answer is zero. But under ASC, we use the (full) time dilation formula (neglecting the first term since v2/c2 is very nearly zero), setting ε = 1. The moving clock will tick slow by a factor of c/(c+v) and it will do this for the duration of the journey (t). So, the total time ticked by the moving clock will be tc/(c+v). But the duration of the journey (t) is simply the distance divided by the velocity (t = D/v). The distance is 186,282.397 miles, which is the round-trip distance light travels in one second. So, the distance is c seconds.[12] Therefore, t = c/v seconds.
Substituting this into our previous expression, we find that the moving clock will tick a total time of c2/v(c+v) seconds during its journey, which lasts c/v seconds. Therefore, the total time lost by the clock during its journey will be c/v – c2/v(c+v) seconds. After some algebra, this reduces to c/(c+v) seconds. And since v is much smaller than c, this further reduces to c/c seconds, which is 1 second. So, under ASC, moving the clock as slowly as possible from A to B will cause it to lose one second.[13]
Under ESC, the two clocks are still synchronized. Light sent from clock A at noon will arrive at clock B at 12:00:01, confirming that outgoing light travels at exactly c and takes one second to traverse the distance. However, under ASC, clock B is now one second behind clock A. And so clock B indeed reads 12:00:01 when the light from A arrives, but the actual time at B is 12:00:02 since that clock is one second slow. Thus, under ASC, the light actually took two seconds to go from A to B, confirming that the outgoing one-way speed of light is exactly ½c. Both conventions predict the same outcome. Therefore, slow clock transport cannot be used to distinguish ASC from ESC.
Virtually all of the proposed experiments that claim to objectively measure the one-way speed of light are some variation of either signal transmission or clock transport. And we have seen that neither method can measure the one-way speed of light without first assuming it. Indeed, even the first successful measurement of the speed of light by Rømer in A.D. 1676 was actually a version of slow clock transport. It cannot measure the one-way speed of light, but it does establish the round-trip speed. We will examine this method and some other attempts to measure the one-way speed of light in the next article.
[1] The ‘conventionality thesis’ is the shortened name of the Reichenbach-Grunbaum thesis of the conventionality of simultaneity.
[2] The situation is analogous to a “perpetual motion machine” – a hypothetical machine that can run indefinitely without requiring any energy input. We know from the laws of thermodynamics that such a machine is impossible. Nonetheless, every year some engineer attempts to patent the blueprints for a perpetual motion machine that he thinks will actually work. But, of course, there is always a flaw. There is always something that the engineer overlooked that would cause the machine to run down over time. But even if we cannot spot the flaw, we know there must be one because of the laws of thermodynamics. Likewise, any hypothetical experiment to objectively measure the one-way speed of light must fail. This is because there is no objective/universal one-way speed of light, nor can there be in a universe in which simultaneity is relative. However, it is instructive to examine some of the proposals, and see why they fail. Examining such failures can lead to a better understanding of the conventionality thesis, and the relativistic nature of time.
[3] Named in honor of Hans Reichenbach who first used this notation.
[4] Radio and light are both the same substance. Namely, they are both electromagnetic waves that come in discrete energy levels called photons. The only different between the two is wavelength/frequency. Radio has a much longer wavelength and much lower frequency than visible light.
[5] We know, for example, that the clocks at A and B can be approximately synchronized using either the ASC or the ESC system. There is only a one second difference between the two over that distance. Therefore, both ESC and ASC will confirm that the round-trip speed of sound in a substance is approximately the same in both directions. The exact speed will of course differ, but the difference will be a smaller fraction for slower phenomena like sound than for rapid phenomena like light.
[6] This is true under both the ESC and ASC system. In fact, the amount by which the moving clock is behind the stationary one is independent of synchrony convention.
[7] A more precise way to say this is, “In the limit as the speed goes to zero, the two clocks approach perfect synchronization when reunited.”
[8] Winnie, J.A., Special Relativity without One-Way Velocity Assumptions: Part I, Philosophy of Science, Vol. 37, No. 1 (March 1970) pp. 81-99.
[9] There is a sign difference in the formula listed here relative to Winnie’s formula 4-9. This is because Winnie defines velocity v to be in the negative x-direction, whereas we here define it to be in the positive x direction. Hence, our v is Winnie’s -v and vice versa.
[10] In the limit as v goes to zero, v2/c2 will go to zero much “faster.”
[11] This right-hand term does not vanish in the limit as v goes to zero because the time (t) it takes to get from A to B goes to infinity in the limit as v goes to zero. The shrinking of v exactly compensates with the growing of t, and therefore neither term can be neglected until the final step.
[12] It may seem strange to refer to a distance in seconds. But when multiplying 1 second by the speed of light (186,282.397 miles / second), the “seconds” in the numerator cancels the “seconds” in the denominator, leaving the distance in miles. So, 186,282.397 miles does indeed equal c seconds.
[13] If we then move the clock at B very slowly back to A, then its velocity will be negative v. Plugging that value into the formula and repeating the above steps we will find that the clock gains one second on its return journey. It will again become synchronized with the stationary clock upon its reunion.

