Infinity is the concept of an unlimited quantity. Although this idea is challenging for us, it is very real because it stems from the mind of God. God’s understanding is infinite (Psalms 147:5). Therefore, to study the nature of infinity is to learn something about the nature of God.
The Logic of Numbers
How can finite minds such as ours possibly know anything about the infinite? How can we reason about a concept that goes beyond our finite ability to conceive? The answer to both questions is revelation. God has revealed some of His thoughts to us. Therefore, we can know about some things that go far beyond our ability to fully grasp.
Eternity is one manifestation of infinity – an infinite amount of time. The Bible teaches that those who have received Christ as Savior and Lord by grace through faith will enjoy eternal life with God (John 3:15-16, 4:14, 5:24, 6:40,47, 10:28). Although we cannot fully grasp the implications of eternity, we have some concept of it because God has placed this concept in our heart – in the core or our being (Ecclesiastes 3:11). We therefore have an awareness of a concept that we cannot fully grasp. Only the biblical worldview can make sense of this.
But how can we reason properly about a subject that we cannot fully comprehend? The answer again is found in revelation. God has gifted us with the tools of logic and mathematics. Logic is the principles of correct reasoning. These principles stem from the mind of God and we have access to them because we are made in God’s image. We can use the principles of logic even in areas that go beyond our ability to fully understand. Mathematics is simply the logic of numbers. We can use mathematics to draw true conclusions about numbers – even when such numbers are infinitely beyond our ability to comprehend! Mathematics is therefore a divine gift that allows us to know truths that our minds cannot fully contain.
The Different Sizes of Infinity
Using the tools of logic that God has gifted to us, we can learn things about infinity that are often counterintuitive to our finite mind. For example, mathematicians have discovered that some types of infinity are “bigger” than other types of infinity. Furthermore, sometimes two sets of infinite numbers are exactly the same size, even if one contains all the numbers of the other set and more! One example of this concerns the counting numbers.
The counting numbers are all the positive integers: 1,2,3,4, and so on. They are infinite in extent because the positive integers never end; you can always add 1 and get the next positive integer. So, the set of all positive integers is infinite. Now consider the set of all integers (both positive and negative, as well as zero). Clearly the set of all integers is infinite because it is unlimited in both the positive and negative direction. Our intuition suggests that the set of all integers is a larger set than the set of only the positive integers. After all, the set of all integers contains all the positive integers and all negative integers and zero. Since one set entirely contains the other as well as numbers that are not in the other, it would have to be bigger, right?
But our intuition is wrong. In fact, the set of all integers is exactly the same size as the set of only the positive integers. Both sets are infinite and they are the same infinity. But how do we know this? One way to show that two sets of numbers are exactly the same size is to show that for every number in one set, there is exactly one number in the other set.

For example, the set containing only 1,2,3, and 4 is the same size as the set containing only 5,6,7, and 8. For each number in the first set there is exactly one number in the second set. One way to show this is to add 4 to each number in the first set and we will have a corresponding number in the second set. That is, 1 corresponds to 5, 2 to 6, 3 to 7, and 4 to 8. Since each number in the first set can be linked to exactly one number in the second set, the two sets are the same size. Using this same method, we can show that each number in the set of all integers matches exactly one number in the set of positive integers.
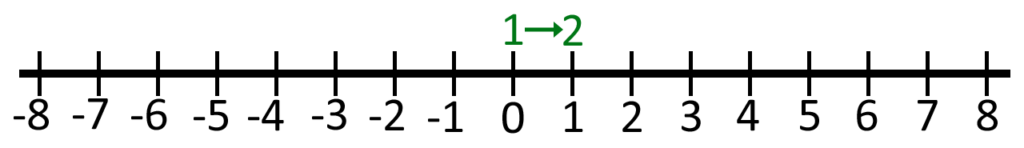
Imagine the set of all integers as displayed on the number line. Starting with zero, we place a number 1 above it. Then we go right to number 1 and place a 2 above it as shown in the figure above. Then we move to negative 1 and place a 3 above it. Then we go to positive 2 and place a 4 above it. Then we go to -2, 3, -3, 4, -4, and so on, each time writing the next positive integer just above the number as illustrated in the figure below. We can see that for each number in the set of all integers, there is a corresponding positive integer (written just above it). We can do this forever in principle without ever running out of numbers. Clearly, for each integer, there is a corresponding positive integer. Therefore, the set of all positive integers is exactly the same size as the set of all integers! Both sets are infinite, and they are exactly the same infinity.
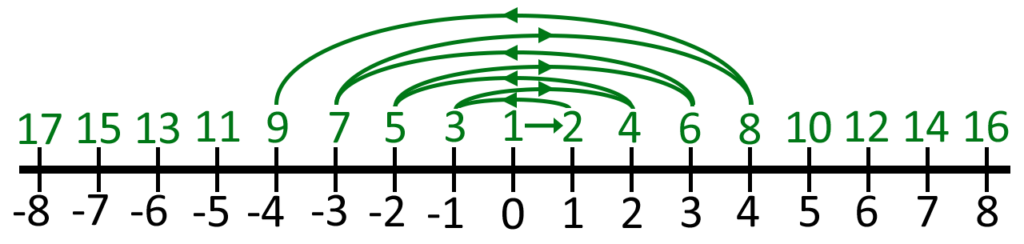
This is deeply counterintuitive because one set completely contains all the numbers in the other, and then some. Yet, the two sets are the same size. This would not be possible for finite sets. But infinity often yields surprising results. Amazingly, the number of rational numbers is the same infinity as the counting numbers. A rational number is any number that can be expressed as the ratio of two integers, as in a/b.
It is perhaps surprising and counterintuitive that rational numbers would be the same infinity as the counting numbers. After all, the rational numbers completely contain all the counting numbers, and an infinite quantity of numbers that are in between them. In fact, there are an infinite number of rational numbers between any two counting numbers. Yet, we can demonstrate from logic that the two sets are the same size. We again do this by showing that there is exactly one positive integer for each rational number. This can be demonstrated geometrically as follows.
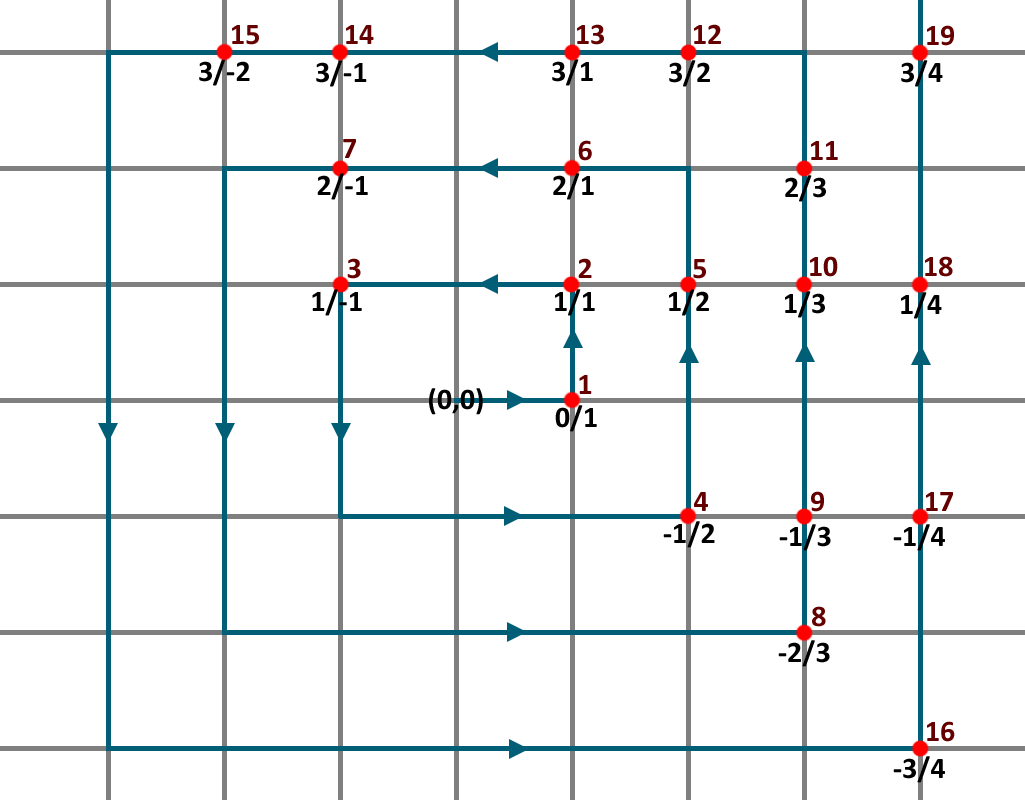
In the figure above, starting at the origin, we move to the coordinates (1,0). Let the x-coordinate (1) represent the denominator of a rational number, and the y-coordinate (0) represent the numerator. So this point represents the rational number 0/1 which is zero. This is the first rational number we have explored, so we label it with counting number 1. Next, we move up to (1,1), representing the rational number 1/1 which is 1. This is the second rational number we have encountered, so we label it 2. We then move left two spaces, and assign the next counting number, then down two, then right three and so on, forming a rectangular spiral pattern (as shown in blue), stopping at each pair of integer coordinates. We skip those coordinates where the denominator would be zero, and we also do not count duplicates. (That is, -2/2 is the same rational number as -1/1. So we do not count it twice.) As we spiral outward, we will eventually hit every possible rational number, since each pair of integer x and y coordinates is eventually crossed. Furthermore, each rational number will be assigned a positive integer. Thus, there is exactly one positive integer for each rational number. Therefore, the set of rational numbers is the same size as the set of counting numbers. They are the same infinity!
Hilbert’s Grand Hotel
The strangeness of infinity is illustrated in a delightful paradox first proposed by David Hilbert in 1924. Imagine a hotel with an infinite number of rooms – one room for each counting number. An infinite number of guests arrive, and each is assigned to one room in the hotel. The hotel is now fully occupied. An additional guest shows up and requests a room. We might at first think that no rooms would be available in a fully occupied hotel. And this would indeed be the case for a hotel with a finite number of rooms. However, the hotel manager is able to accommodate the request by asking each guest to move to the next room. That is, the person in room 1 moves to room 2, the person in room 2 moves to room 3 and so on. Since there is no “last” room in an infinite hotel, each guest is able to do this, which leaves room 1 empty and available for the new guest.
But suppose an infinite number of additional people show up the same evening. Each room in the hotel is already occupied, and yet the hotel manager is again able to accommodate the new visitors in the following way. He asks each person already in a hotel room to move to the room that is twice the number of the current room. So the person in room 1 moves to room 2, the person in room 2 moves to room 4, and so on. This leaves all the odd numbered rooms unoccupied. And since there are an infinite number of odd rooms, each of the new visitors is assigned to one of these rooms and the hotel is again fully occupied.
The infinity we have discussed so far is countable. Countable means that if you started counting 1,2,3,4, and continued forever, you would eventually hit every positive integer. This is the smallest possible infinity.[1] Its “size” or cardinality is represented by the Hebrew letter aleph with a subscript zero (א0), and pronounced “aleph naught.” However, not all infinities are countable. There are some infinite sets where even if you spent all eternity counting their elements, there would still be an infinite number that you could never count. Uncountable infinities are therefore larger than countable infinities; that is, they have a larger cardinality.
Uncountable Infinities
One example of an uncountable infinity is the quantity of real numbers. The real numbers include both the rational and irrational numbers. In mathematics, an irrational number is one that cannot be expressed as the ratio of two finite integers such as a/b. The decimal expression of an irrational number goes on forever without settling on any infinitely repeating sequence. Perhaps the most well-known irrational number is pi: the ratio of the circumference to diameter in a circle. The decimal expression of pi continues forever without a recognizable pattern: 3.1415926535897932384626433… Other irrational numbers include Euler’s number (e) as well as the square-root of any integer that is not itself an integer, e.g. the square-root of 2.
How can we prove that the set of real numbers is a larger infinity than the countable numbers? We do this by a reductio ad absurdum. This is the method of demonstrating that a claim is false by assuming (for the sake of argument) that it is true and showing how this would lead to a contradiction. So, we assume for the sake of hypothesis that we can list the real numbers in such a way that each one is assigned to exactly one counting number. To make this more tractable, we will consider only the real numbers between zero and one. If this is a greater infinity than the countable numbers, then so must be the infinity of all real numbers which includes this list.
The order of the real numbers would have to be random because there is an infinite quantity of numbers in between any two real numbers. But let’s assume that each and every real number between 0 and 1 is on this list in the right-hand column of the figure below. And each corresponds to exactly one positive integer in the left-hand column.

Now, we are going to construct a real number by the following method. Take the first digit of the first number on the right-hand column (shown in red) and pick any number except that one. The first digit of the first number is 1, so let’s pick 2. Now look at the second digit of the second number on the list (also in red) and pick any number except that one. So let’s pick 9. Then we examine the third digit of the third number, and pick a different number, and so on. If we were to do this forever, we would end up with a real number between zero and one, such as 0.29941362260062624….
However, this number we have constructed cannot be in the right-hand column because it differs by at least one digit in one location from every number on this list! Yet, we stipulated at the outset that the right-hand column contained every real number between zero and one, each corresponding to one positive integer. We have reached a contradiction since we have constructed a real number between 0 a 1 that is not on this list. Therefore, we now see that such a list cannot exist, because we can always construct a real number that is not on this list by changing one number in each digit from numbers that are on the list. Therefore, our initial claim (that there can be a list of real numbers with each one corresponding to a positive integer) is disproved. There will always be real numbers that are not on such a list.
Thus, the quantity of real numbers (between zero and one) is greater than the quantity of positive integers. And since the set of all real numbers includes the set of real numbers between zero and one, it too is a larger infinity than the set of positive integers. The set of all real numbers is therefore a non-countable infinity. It is larger than א0. In fact, the cardinality of real numbers has been proved to be 2 to the power of א0. Could the real numbers represent the second smallest infinity? Many mathematicians suspect this is the case, but it is unproved. The concept is called the continuum hypothesis. If it is correct, then the quantity of real numbers is indeed the second smallest infinity and designated as א1. If so, then there is no set with a cardinality between that of the integers and the real numbers.
It is truly remarkable that we can reason and draw correct conclusions about infinity. After all, our minds are finite. Yet, the laws of logic and mathematics by which we reason are useful even in areas that we cannot fully grasp. This is because such laws reflect the thinking of the Lord. And by His grace, He has allowed us to use these laws to reason correctly about things that are infinitely beyond us. Only the biblical worldview can make sense of this truth. Glory be to God!
[1] That א0 is the smallest possible infinity is based on the axiom of countable choice.

