We have been analyzing the claims of Phillip Dennis and his criticism of the ASC model. In particular, Dennis claims to have refuted the conventionality thesis – Einstein’s claim that the one-way speed of light “is in reality neither a supposition nor a hypothesis about the physical nature of light, but a stipulation which I can make of my own freewill in order to arrive at a definition of simultaneity” [emphasis in original] (Einstein 1916). Conversely, Dennis claims that Einstein is wrong and that the one-way speed of light is necessarily the same as the round-trip speed of light: c = 186,282.397 miles per second in vacuum. However, we have already shown that Dennis’s previous attempts to prove this were fallacious because they begged the question. That is, Dennis had used equations that tacitly assume the one-way speed of light. In his latest article, Dennis claims that the one-way speed of light has been empirically measured in two independent experiments. We will examine the first of these here. We will again show that Dennis has once again begged the question. That is, he unwittingly assumed the one-way speed of light is isotropic in his argument.
The Laser Experiment
Dennis begins his analysis with a strawman fallacy – a misrepresentation of my position. He states, “We shall begin with the perpetuated myth that it is impossible to measure a one-way speed of light” (Dennis 2024). In fact, my position is that it is impossible to measure a one-way speed of light without first tacitly assuming/stipulating it. This is a crucial distinction and is the entire point of the conventionality thesis, yet Dennis continues to miss it. Of course, we can assume/stipulate the one-way speed of light in any one direction, then use that stipulation to synchronize two clocks separated by a distance, and then use those two clocks to measure the one-way speed of light. The answer we get will be exactly what we stipulated to begin with. That’s the point. And we will see that this is exactly what Dennis did in his analysis of an experiment. He assumed that the one-way speed of light is the same in all directions at the start – the very thing he is supposed to be proving! Let’s look at the experiment.
There have been many experiments in which a laser/light pulse travels through a substance and is filmed at ultra-high speed. Dennis mentions such an experiment and concludes that this measures the one-way speed of light. Unfortunately, he does not specify which of these experiments he gets his numbers from, nor does he provide a reference. So there is no way to know which exact experiment he refers to. Nevertheless, there are many experiments of this kind and we will demonstrate here that none of them can, even in principle, measure the one-way speed of light without first assuming it. Here is an example of the kind of experiment Dennis references:
https://www.youtube.com/watch?v=-fSqFWcb4rE
In the video of the link above, we see a light pulse traveling through a soda bottle that is filled with water. The video is filmed at a rate of 1 trillion frames per second and is apparently played back at a rate of about 60 frames per second in the first animation.[1] Thus, we see the video slowed by a factor of 17 billion times. It takes about 15 playback seconds for the pulse to traverse the bottle, which is around 20 centimeters in length. So the actual speed of light in the water would seem to be 2.2 × 108 m/s. Dennis arrives at a similar number (2.264 × 108 m/s) from whatever experiment he was analyzing. He incorrectly labels this as “c”; however, c always refers to the round-trip speed of light in vacuum (c = 2.9979 × 108 m/s), not the speed in water which is slower.
And since the light beam goes in only one direction, from left to right, it seems we have measured the speed of light in only one direction without first assuming it! Indeed, Dennis claims, “This is a very precise value measurement of a one-way speed of light” (Dennis 2024). But is it really? Consider very carefully the following question: How is the camera able to detect the light?
In other words, the camera does not magically report the position of the light in the bottle and create a picture of it. Cameras can only detect light that enters their lens and lands on their detector just as our eyes can only detect light that enters them. So how does the light in the bottle land on the detector?
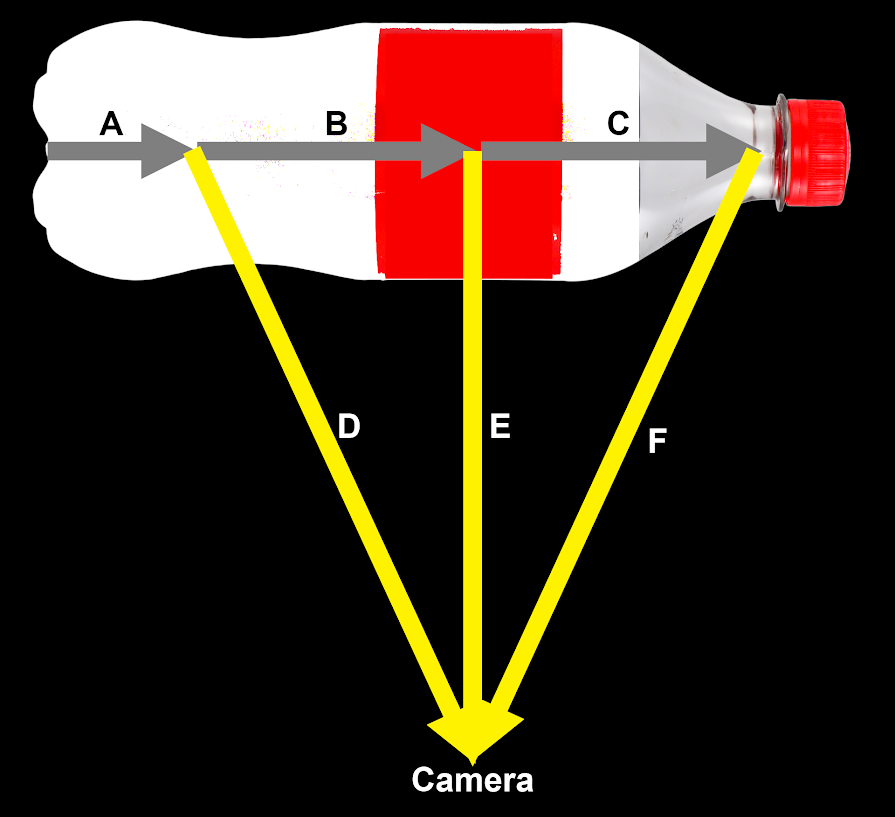
In order for the camera to film the light, some of the light from the pulse must reflect off particles in the water and be redirected so that it enters the camera. Such paths are shown in yellow in Figure 1. If the light pulse went through the water in the bottle, and none of it reflected and then went toward the camera, then the camera would not see the light at all. Therefore, every image of the light that is detected by the camera has been reflected into a second path that intersects the camera. This is illustrated in Figure 1. To be seen by the camera, a light pulse has to first travel along the gray path (one way) and then along the (different) yellow path (another way). Hence, it is not a pure one-way speed test.
Early in the experiment, nearly all the light travels along path A, but a small fraction is reflected off particles in the water and now takes path D toward the camera. The camera detects only this light at this time. The rest of the light continues along path B until some is reflected and now travels along path E to be detected by the camera. The remaining light in the bottle travels along path C, and a small fraction is reflected off particles in the water and redirected along path F. The camera is able to “see” light traveling along A, B, and C only because a small fraction of it has traveled along paths D, E, and F.
Dennis’s Mistake
Dennis seems to have falsely assumed that this experiment is only measuring the time it takes the light to traverse the paths A, B, and C, but he has forgotten to include the time it takes light to traverse the paths D, E, and F, in order to reach the camera. Or perhaps he assumes those times are all the basically the same – but that assumes ESC! ESC stipulates that the one-way speed of light is the same in all directions. Under any synchrony convention except ESC, the velocity of light has directional dependence. Clearly, paths D, E, and F, have different directions, and therefore the speed of light along them potentially will be different for any convention other than ESC. So in neglecting the travel time of the light along paths D, E, and F, Dennis has unwittingly assumed the ESC convention (and the one-way speed of light) – the very thing he is supposed to be proving!
In fact, Dennis did not even bother to go through the math to see if ASC would give the same answer (as it must) as ESC regarding the observations of the light through a bottle. He arbitrarily assumed that this observation is incompatible with ASC. But he didn’t demonstrate this. This is an example of confirmation bias – the same basic error Dennis committed in his previous publication. So let’s do what Dennis failed to do and compute the observational results of this kind of experiment using ASC, to see if it actually gives a different answer than what Dennis has arbitrarily assumed.
The Correct Analysis
For simplicity, let’s consider this experiment in the vacuum of space rather than water. (The ASC model deals with the one-way speed of light in vacuum; we would need to adjust the formula to deal with the speed of light in a substance because it is slower.) So the soda bottle is empty except for a smattering of dust particles to scatter the light pulse so it can be detected by the camera. Let’s suppose the camera is 100 cm away from the center of the bottle, and that the bottle is exactly 20 cm long. We’ll consider path A to be negligible so that when the light first strikes the bottle, some of it is redirected along path D. Path B takes the light directly to the center of the bottle, 10 cm away, where some is redirected at a right angle along path E. Path C is 10 cm long and takes us to the end of the bottle where some of the light is redirected along path F. How long does it take for the camera to see the light traverse the width of the bottle? Mathematically, this will be the time it took the light to traverse the path A and B and C and F minus the time it took the light to traverse path A and D. And we have stipulated that path A is negligible. So the time will be TB + TC + TF – TD.
First, let’s analyze the situation using ESC coordinates. Then the speed of light along any length is exactly c (2.9979 × 108 m/s). Since paths B and C are 10 cm each, then TB = TC = 3.336 × 10-10 seconds. By the Pythagorean theorem, paths D and F are each 100.499 cm long. Therefore, TF = TD = 3.352 × 10-9 seconds. Adding these up we find: TB + TC + TF – TD = 6.672 × 10-10 seconds.
So according to ESC, the light pulse will appear to take 6.672 × 10-10 seconds to traverse the bottle.
Now let’s analyze the same scenario using ASC. In ASC, the one-way speed of light depends on the direction relative to the observer, with light that is directly incoming being instantaneous. Let’s imagine that the observer is far below the camera in the negative y direction according to Figure 1. (So light traveling directly in the negative y direction is instantaneous.) For all other angles, the velocity of the one-way speed of light is given by the following formula: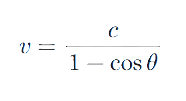
Here, θ is the angle between the light vector and line that is directly toward the observer. So θ = 0 for light that is directly in the negative y direction. For paths (A), B, and C, θ = 90° and so the speed of light along paths (A), B, and C is exactly c. Therefore, TB = TC = 3.336 × 10-10 just as before. However, for paths D and F, cos θ = 100/100.499, (θ = 5.712°). The speed of light along paths D and F will be 6.0378 × 1010 m/s, and therefore TF = TD = 1.665 × 10-11 s. Adding up these values we get: TB + TC + TF – TD = 6.672 × 10-10 seconds.
So according to ASC, the light pulse will appear to take 6.672 × 10-10 seconds to traverse the bottle – exactly the same value as with ESC.
Amazingly, this works no matter where the observer is – no matter which direction we select to be the one in which the speed of light is instantaneous. Suppose, for example, that the observer is far to the right of the bottle so that the light traveling through the bottle is directly toward the observer. Then the light along the positive x axis moves infinitely fast, and the angle θ now represents the departure from the x axis.
In this scenario, the light takes no time at all to traverse paths B and C because θ = 0. That is, TB = TC = 0. So the light zips along the bottle instantaneously. But is this what the camera will detect? In this case, the light along path D travels at an angle relative to the positive x axis. The angle is given by cos θ = 10/100.499 (and therefore θ = 84.29°). So the one-way speed of light along path D will be 3.3292 × 108 m/s, and therefore TD = 3.0187× 10-9 seconds. However, the light along path F travels at a different angle given by cos θ = -10/100.499 (and therefore θ = 95.71°). Therefore, the light will travel along F with speed 2.7266 × 108 m/s. Notice that the light travels slower along path F than along path D because F departs more from the positive x direction. So although both light beams (along D and F) start their journey at the same time, the light along F will arrive at a later time. Using the speed of light along F, we compute TF = 3.6859× 10-9 seconds. So what do we get for the total time observed by the camera? TB + TC + TF – TD = 6.672 × 10-10 seconds.
Once again, according to ASC, the light pulse will appear to take 6.672 × 10-10 seconds to traverse the bottle – exactly the same value as with ESC!
So even when the one-way speed of light is instantaneous along the direction of the bottle, the camera still sees exactly the same result. Any differences between ASC and ESC along paths A, B, and C are exactly compensated along paths D, E, and F. This is because the round-trip speed of light is constant in vacuum. The one-way speed is a humanly stipulated convention that allows us to define simultaneity for some group of observers. So Einstein was right, and Dennis is wrong.
Conclusions
Dennis didn’t bother to do these calculations. He simply assumed that if the light beam looks like it takes time to travel along A, B, and C, then it must really be that way since light travels the same speed in all directions. But this begs the question! Dennis neglected to account for paths D, E, and F. He neglected to check whether ASC coordinates would give the same results – the confirmation bias. When we do the math properly, we find that these kinds of experiments confirm the conventionality thesis and refute Dennis’s fallacious reasoning.
[1] A later animation in the same video appears to play back at 15 frames per second and is therefore 4 times longer than the first animation.